Trigonometric function
|
|
In mathematics, the trigonometric functions are functions of an angle, important when studying triangles and modeling periodic phenomena. They may be defined as ratios of two sides of a right triangle containing the angle, or, more generally, as ratios of coordinates of points on the unit circle, or, more generally still, as infinite series, or equally generally, as solutions of certain differential equations. All four approaches will be presented below. In all of these cases referring to triangles, the triangles are taken to exist in the Euclidean plane, so that the angles always sum to 180°.
In modern usage, there are six basic trigonometric functions, which are tabulated below along with equations relating them to one another. (Especially in the case of the last four, these relations are often taken as the definitions of those functions, but one can equally define them geometrically or by other means and derive the relations.)
| Function | Abbreviation | Relation |
|---|---|---|
| Sine | sin | <math>\sin \theta = \cos \left(\frac{\pi}{2} - \theta \right) \,<math> |
| Cosine | cos | <math>\cos \theta = \sin \left(\frac{\pi}{2} - \theta \right)\,<math> |
| Tangent | tan | <math>\tan \theta = \frac{\sin \theta}{\cos \theta} \,<math> |
| Cotangent | cot | <math>\cot \theta = \frac{1}{\tan \theta} = \frac{\cos \theta}{\sin \theta} = \tan \left(\frac{\pi}{2} - \theta \right) \,<math> |
| Secant | sec | <math>\sec \theta = \frac{1}{\cos \theta} \,<math> |
| Cosecant | csc | <math>\csc \theta =\frac{1}{\sin \theta} = \sec \left(\frac{\pi}{2} - \theta \right) \,<math> |
A few other functions were common historically (and appeared in the earliest tables), but are now little-used, such as the versed sine (versin = 1 − cos) and the exsecant (exsec = sec − 1).
Many more relations between these functions are listed in the article about trigonometric identities.
| Contents |
Right triangle definitions
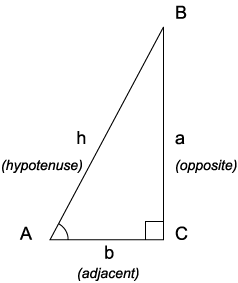
In order to define the trigonometric functions for the angle A, start with an arbitrary right triangle that contains the angle A:
We use the following names for the sides of the triangle:
- The hypotenuse is the side opposite the right angle, or defined as the longest side of a right-angled triangle, in this case h.
- The opposite side is the side opposite to the angle we are interested in, in this case a.
- The adjacent side is the side that is in contact with the angle we are interested in and the right angle, hence its name. In this case the adjacent side is b.
Then,
1). The sine of an angle is the ratio of the length of the opposite side to the length of the hypotenuse. In our case
- sin(A) = opp/hyp = a/h.
Note that this ratio does not depend on the particular right triangle chosen, as long as it contains the angle A, since all those triangles are similar.
2). The cosine of an angle is the ratio of the length of the adjacent side to the length of the hypotenuse. In our case
- cos(A) = adj/hyp = b/h.
3). The tangent of an angle is the ratio of the length of the opposite side to the length of the adjacent side. In our case
- tan(A) = opp/adj = a/b.
The remaining three functions are best defined using the above three functions.
4). The cosecant csc(A) is the multiplicative inverse of sin(A), i.e. the ratio of the length of the hypotenuse to the length of the opposite side:
- csc(A) = hyp/opp = h/a.
5). The secant sec(A) is the multiplicative inverse of cos(A), i.e. the ratio of the length of the hypotenuse to the length of the adjacent side:
- sec(A) = hyp/adj = h/b.
6). The cotangent cot(A) is the multiplicative inverse of tan(A), i.e. the ratio of the length of the adjacent side to the length of the opposite side:
- cot(A) = adj/opp = b/a.
Mnemonics
There are a number of mnemonics for the above definitions, for example SOHCAHTOA (sounds like "soak a toe-a", can be read as "soccer tour"). It reminds one that:
- SOH ... sin = opposite/hypotenuse
- CAH ... cos = adjacent/hypotenuse
- TOA ... tan = opposite/adjacent.
Many other such words and phrases have been contrived; for more, see: trigonometry mnemonics.
Computation
The computation of trigonometric functions is a complicated subject, which can today be avoided by most people because of the widespread availability of computers and scientific calculators that provide built-in trigonometric functions for any angle. In this section, however, we describe more details of their computation in three important contexts: the historical use of trigonometric tables, the modern techniques used by computers, and a few "important" angles where simple exact values are easily found. (Below, it suffices to consider a small range of angles, say 0 to π/2, since all other angles can be reduced to this range by the periodicity and symmetries of the trigonometric functions.)
Prior to computers, people typically evaluated trigonometric functions by interpolating from a detailed table of their values, calculated to many significant figures. Such tables have been available for as long as trigonometric functions have been described (see History, below), and were typically generated by repeated application of the half-angle and angle-addition identities starting from a known value (such as sin(π/2)=1). See also: Generating trigonometric tables.
Modern computers use a variety of techniques (Kantabutra, 1996). One common method, especially on higher-end processors with floating point units, is to combine a polynomial approximation (such as a Taylor series or a rational function) with a table lookup — they first look up the closest angle in a small table, and then use the polynomial to compute the correction. On simpler devices that lack hardware multipliers, there is an algorithm called CORDIC (as well as related techniques) that is more efficient, since it uses only shifts and additions. All of these methods are commonly implemented in hardware for performance reasons.
Finally, for some simple angles, the values can be easily computed by hand using the Pythagorean theorem, as in the following examples. In fact, the sine, cosine and tangent of any integer multiple of three degrees (π/60 radians) can be found exactly by hand.
Consider a right triangle where the two other angles are equal, and therefore are both 45 degrees (π/4 radians). Then the length of side b and the length of side a are equal; we can choose a = b = 1. The values of sine, cosine and tangent of an angle of 45 degrees can then be found using the Pythagorean theorem, c = √(a2 + b2) = √2. Therefore,
- <math>\sin \left(45^\circ\right) = \sin \left(\pi / 4 \right) = \cos \left(45^\circ\right) = \cos \left(\pi / 4 \right) = {1 \over \sqrt2}<math>
- <math>\tan \left(45^\circ\right) = \tan \left(\pi / 4 \right) = {\sqrt2 \over \sqrt2} = 1<math>
To determine the trigonometric functions for angles of 60 degrees (π/3 radians) and 30 degrees (π/6 radians), we start with an equilateral triangle of side length 1. All its angles are 60 degrees. By dividing it into two, we obtain a right triangle with 30 and 60 degree angles. For this triangle, the shortest side = 1/2, the next largest side =(√3)/2 and the hypotenuse = 1. This yields:
- <math>\sin \left(30^\circ\right) = \sin \left(\pi / 6 \right) = \cos \left(60^\circ\right) = \cos \left(\pi / 3 \right) = {1 \over 2}<math>
- <math>\cos \left(30^\circ\right) = \cos \left(\pi / 6 \right) = \sin \left(60^\circ\right) = \sin \left(\pi / 3 \right) = {\sqrt3 \over 2}<math>
- <math>\tan \left(30^\circ\right) = \tan \left(\pi / 6 \right) = \cot \left(60^\circ\right) = \cot \left(\pi / 3 \right) = {1 \over \sqrt3}<math>
See also: Exact trigonometric constants
Unit-circle definitions
The six trigonometric functions can also be defined in terms of the unit circle, the circle of radius one centered at the origin. The unit circle definition provides little in the way of practical calculation; indeed it relies on right triangles for most angles. The unit circle definition does, however, permit the definition of the trig functions for all positive and negative arguments, not just for angles between 0 and π/2 radians. It also provides a single visual picture that encapsulates at once all the important triangles used so far. The equation for the unit circle is: <math>x^2 + y^2 = 1<math>
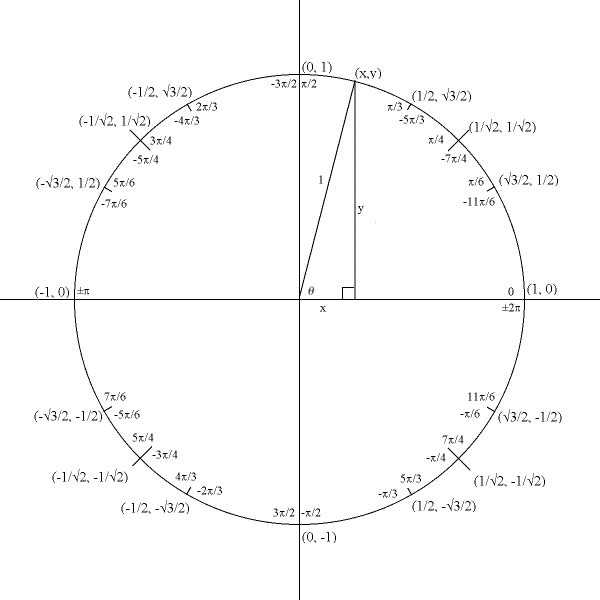
In the picture, some common angles, measured in radians, are given. Note that we measure angles positive in the counter clockwise direction and angles negative in the clockwise direction. Let a line making an angle of θ with the positive half of the x-axis intersect the unit circle. The x- and y-coordinates of this point of intersection are equal to cos θ and sin θ, respectively. The triangle in the graphic reveals the reason: the radius is equal to the hypotenuse and has length 1, so we have sin θ = y/1 and cos θ = x/1. The unit circle can be thought of as a way of looking at an infinite number of triangles by varying the lengths of their legs but keeping the lengths of their hypotenuses equal to 1.
For angles greater than 2π or less than −2π, simply continue to rotate around the circle. In this way, sine and cosine become periodic functions with period 2π:
- <math>\sin\theta = \sin\left(\theta + 2\pi k \right)<math>
- <math>\cos\theta = \cos\left(\theta + 2\pi k \right)<math>
for any angle θ and any integer k.
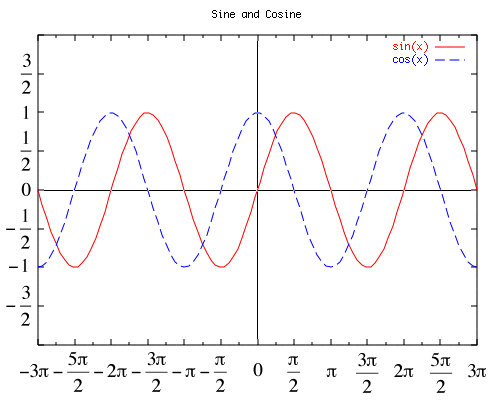
The smallest positive period of a periodic function is called the primitive period of the function. The primitive period of the sine, cosine, secant, or cosecant is a full circle, i.e. 2π radians or 360 degrees; the primitive period of the tangent or cotangent is only a half-circle, i.e. π radians or 180 degrees.
Above, only sine and cosine were defined directly by the unit circle, but the other four trig functions can be defined by:
- <math>\tan\theta = \frac{\sin\theta}{\cos\theta}<math>
- <math>\sec\theta = \frac{1}{\cos\theta}<math>
- <math>\csc\theta = \frac{1}{\sin\theta}<math>
- <math>\cot\theta = \frac{\cos\theta}{\sin\theta}<math>
Circle-trig6.png
Alternatively, all of the basic trigonometric functions can be defined in terms of a unit circle centered at O (shown at right), and similar such geometric definitions were used historically. In particular, for a chord AB of the circle, where θ is half of the subtended angle, sin(θ) is AC (half of the chord), a definition introduced in India (see below). cos(θ) is the horizontal distance OC, and versin(θ) = 1 − cos(θ) is CD. tan(θ) is the length of the segment AE of the tangent line through A, hence the word tangent for this function. cot(θ) is another tangent segment, AF. sec(θ) = OE and csc(θ) = OF are segments of secant lines (intersecting the circle at two points), and can also be viewed as projections of OA along the tangent at A to the horizontal and vertical axes, respectively. DE is exsec(θ) = sec(θ) − 1 (the portion of the secant outside, or ex, the circle). From these constructions, it is easy to see that the secant and tangent functions diverge as θ approaches π/2 (90 degrees) and that the cosecant and cotangent diverge as θ approaches zero. (Many similar constructions are possible, and the basic trigonometric identities can also be proven graphically.)
Here is a plot of sine and cosine:
Series definitions
Please note: Here, and generally in calculus, it is of utmost importance that all angles are measured in radians.
Using only geometry and properties of limits, it can be shown that the derivative of sine is cosine and the derivative of cosine is negative sine. One can then use the theory of Taylor series to show that the following identities hold for all real numbers x:
- <math>\sin x = x - \frac{x^3}{3!} + \frac{x^5}{5!} - \frac{x^7}{7!} + \cdots = \sum_{n=0}^\infty \frac{(-1)^nx^{2n+1}}{(2n+1)!}<math>
- <math>\cos x = 1 - \frac{x^2}{2!} + \frac{x^4}{4!} - \frac{x^6}{6!} + \cdots = \sum_{n=0}^\infty \frac{(-1)^nx^{2n}}{(2n)!}<math>
These identities are often taken as the definitions of the sine and cosine function. They are often used as the starting point in a rigorous treatment of trigonometric functions and their applications (e.g. in Fourier series), since the theory of infinite series can be developed from the foundations of the real number system, independent of any geometric considerations. The differentiability and continuity of these functions are then established from the series definitions alone.
Relationship to exponential function
It can be shown that the sine and cosine functions are the imaginary and real parts, respectively, of the complex exponential function when its argument is purely imaginary:
- <math> e^{i \theta} = \cos\theta + i\sin\theta \,.<math>
This relationship was first noted by Euler and the identity is called Euler's formula. In this way, trigonometric functions become essential in the geometric interpretation of complex analysis. For example, with the above identity, if one considers the unit circle in the complex plane, defined by eix, and as above, we can parametrize this circle in terms of cosines and sines, the relationship between the complex exponential and the trigonometric functions becomes more apparent.
Furthermore, this allows for the definition of the trigonometric functions for complex arguments z:
- <math>\sin z \, = \, \sum_{n=0}^{\infty}\frac{(-1)^{n}}{(2n+1)!}z^{2n+1} \, = \, {e^{\imath z} - e^{-\imath z} \over 2\imath} = -\imath \sinh \left( \imath z\right) <math>
- <math>\cos z \, = \, \sum_{n=0}^{\infty}\frac{(-1)^{n}}{(2n)!}z^{2n} \, = \, {e^{\imath z} + e^{-\imath z} \over 2} = \cosh \left(\imath z\right)<math>
where i2</sub> = −1. Also, for purely real x,
- <math>\cos x \, = \, \mbox{Re } (e^{\imath x})<math>
- <math>\sin x \, = \, \mbox{Im } (e^{\imath x})<math>
It is also shown that exponential processes are intimately linked to periodic behavior.
Definitions via differential equations
Both the sine and cosine functions satisfy the differential equation
- <math>y\,''=-y<math>
i.e. each is the additive inverse of its own second derivative. Within the 2-dimensional vector space V consisting of all solutions of this equation, the sine function is the unique solution satisfying the initial conditions y(0) = 0 and y′(0) = 1, and the cosine function is the unique solution satisfying the initial conditions y(0) = 1 and y′(0) = 0. Since the sine and cosine functions are linearly independent, together they form a basis of V. This method of defining the sine and cosine functions is essentially equivalent to using Euler's formula. (See linear differential equation.) It turns out that this differential equation can be used not only to define the sine and cosine functions but also to prove the trigonometric identities for the sine and cosine functions. See the trigonometric identity article for this technique.
The tangent function is the unique solution of the nonlinear differential equation
- <math>y\,'=1+y^2<math>
satisfying the initial condition y(0) = 0. There is a very interesting visual proof that the tangent function satisfies this differential equation; see [1] (http://www.usfca.edu/vca/PDF/vca-preface.pdf).
Inverse functions
The trigonometric functions are periodic, so we must restrict their domains before we are able to define a unique inverse. In the following, the functions on the left are defined by the equation on the right; these are not proved identities. The principal inverses are usually defined as:
- <math> \begin{matrix}
\mbox{for} & -\frac{\pi}{2} \le y \le \frac{\pi}{2},
& y = \arcsin(x) & \mbox{if and only if} & x = \sin(y) \\
\mbox{for} & 0 \le y \le \pi,
& y = \arccos(x) & \mbox{if and only if} & x = \cos(y) \\
\mbox{for} & -\frac{\pi}{2} < y < \frac{\pi}{2},
& y = \arctan(x) & \mbox{if and only if} & x = \tan(y) \\
\mbox{for} & -\frac{\pi}{2} \le y \le \frac{\pi}{2}, y \ne 0,
& y = \arccsc(x) & \mbox{if and only if} & x = \csc(y) \\
\mbox{for} & 0 \le y \le \pi, y \ne \frac{\pi}{2},
& y = \arcsec(x) & \mbox{if and only if} & x = \sec(y) \\
\mbox{for} & -\frac{\pi}{2} < y < \frac{\pi}{2}, y \ne 0,
& y = \arccot(x) & \mbox{if and only if} & x = \cot(y) \\
\end{matrix} <math>
For inverse trigonometric functions, the notations sin− 1 and cos− 1 are often used for arcsin and arccos, etc. When this notation is used, the inverse functions are sometimes confused with the multiplicative inverses of the functions. Our notation avoids such confusion.
These functions may also be defined by proving that they are antiderivatives of other functions. Then each function is uniquely determined by its value at a single point:
- <math>\arcsin\left(z\right) =
\int \frac 1 {\sqrt{1 - z^2}}\,dz + C<math>
- <math>\arccos\left(z\right) =
\int \frac {-1} {\sqrt{1 - z^2}}\,dz + C<math>
- <math>\arctan\left(z\right) =
\int \frac 1 {1 + z^2}\, dz + C<math>
- <math>\arccsc\left(z\right) =
\int \frac {-1} {z^2 \sqrt{1 - \frac{1}{z^2}} }\, dz + C<math>
- <math>\,\arcsec\left(z\right) =
\int \frac 1 {|z| \sqrt{z^2 - 1}}\, dz + C<math>
- <math>\arccot\left(z\right) =
\int \frac {-1} {z^2 + 1}\, dz + C<math>
Note: arcsec can also mean arcsecond.
Identities
- <math>\sin \left(x+y\right)=\sin x \cos y + \cos x \sin y<math>
- <math>\sin \left(x-y\right)=\sin x \cos y - \cos x \sin y<math>
- <math>\cos \left(x+y\right)=\cos x \cos y - \sin x \sin y<math>
- <math>\cos \left(x-y\right)=\cos x \cos y + \sin x \sin y<math>
- <math>\sin x+\sin y=2\sin \frac{x+y}{2}\cos \frac{x-y}{2}<math>
- <math>\sin x-\sin y=2\cos \frac{x+y}{2}\sin \frac{x-y}{2}<math>
- <math>\cos x+\cos y=2\cos \frac{x+y}{2}\cos \frac{x-y}{2}<math>
- <math>\cos x-\cos y=-2\sin \frac{x+y}{2}\sin \frac{x-y}{2}<math>
- <math>\tan x+\tan y=\frac{\sin \left( x+y\right) }{\cos x\cos y}<math>
- <math>\tan x-\tan y=\frac{\sin \left( x-y\right) }{\cos x\cos y}<math>
- <math>\cot x+\cot y=\frac{\sin \left( x+y\right) }{\sin x\sin y}<math>
- <math>\cot x-\cot y=\frac{-\sin \left( x-y\right) }{\sin x\sin y}<math>
See also trigonometric identity.
Properties and applications
The trigonometric functions, as the name suggests, are of crucial importance in trigonometry, mainly because of the following two results:
The law of sines for an arbitrary triangle states:
- <math>\frac{\sin(A)}{a} = \frac{\sin(B)}{b} = \frac{\sin(C)}{c}<math>
It can be proven by dividing the triangle into two right ones and using the above definition of sine. The common number sin(A)/a occurring in the theorem is the reciprocal of the diameter of the circle through the three points A, B and C. The law of sines is useful for computing the lengths of the unknown sides in a triangle if two angles and one side are known. This is a common situation occurring in triangulation, a technique to determine unknown distances by measuring two angles and an accessible enclosed distance.
The law of cosines is an extension of the Pythagorean theorem:
- <math>c^2=a^2+b^2-2ab\cos(C) \,\!<math>
Again, this theorem can be proven by dividing the triangle into two right ones. The law of cosines is useful to determine the unknown data of a triangle if two sides and an angle are known.
If the angle is not contained between the two sides, the triangle may not be unique. Be aware of this ambiguous case of the Cosine law.
There is also a law of tangents:
- <math>\frac{a+b}{a-b} = \frac{\tan[\frac{1}{2}(A+B)]}{\tan[\frac{1}{2}(A-B)]}<math>
The trigonometric functions are also important outside of the study of triangles. They are periodic functions with characteristic wave patterns as graphs, useful for modelling recurring phenomena such as sound or light waves. Every signal can be written as a (typically infinite) sum of sine and cosine functions of different frequencies; this is the basic idea of Fourier analysis, where trigonometric series are used to solve a variety of boundary-value problems in partial differential equations.
Sincos_pretty.png
The image on the right displays a two-dimensional graph based on such a summation of sines and cosines, illustrating the fact that arbitrarily complicated closed curves can be described by a Fourier series. Its equation is:
- <math>(x(\theta),\,y(\theta)) = \sum_{n=1}^\infty \frac {1}{F(n+1)} (\sin(\theta\cdot F(n)),\, \cos(\theta\cdot F(n))) <math>
where F(n) is the nth Fibonacci number.
For a compilation of many relations between the trigonometric functions, see trigonometric identities.
History
The earliest systematic study of trigonometric functions and tabulation of their values was performed by Hipparchus of Nicaea (180-125 BC), who tabulated the lengths of circle arcs (angle A times radius r) with the lengths of the subtending chords (2r sin(A/2)). Later, Ptolemy (2nd century) expanded upon this work in his Almagest, deriving addition/subtraction formulas for the equivalent of sin(A + B) and cos(A + B). Ptolemy also derived the equivalent of the half-angle formula sin(A/2)2 = (1 − cos(A))/2, allowing him to create tables with any desired accuracy. Neither the tables of Hipparchus nor of Ptolemy have survived to the present day.
The next significant development of trigonometry was in India, in the works known as the Siddhantas (4th–5th century), which first defined the sine as the modern relationship between half an angle and half a chord. The Siddhantas also contained the earliest surviving tables of sine values (along with 1 − cos values), in 3.75-degree intervals from 0 to 90 degrees.
The Hindu works were later translated and expanded by the Arabs, who by the 10th century (in the work of Abu'l-Wefa) were using all six trigonometric functions, and had sine tables in 0.25-degree increments, to 8 decimal places of accuracy, as well as tables of tangent values.
Our modern word sine comes, via sinus ("bay" or "fold") in Latin, from a mistranslation of the Sanskrit jiva (or jya). jiva (originally called ardha-jiva, "half-chord", in the 6th century Aryabhatiya) was transliterated by the Arabs as jiba (جب), but was confused for another word, jaib (جب) ("bay"), by European translators such as Robert of Chester and Gherardo of Cremona in Toledo in the 12th century, probably because jiba (جب) and jaib (جب) are written the same in Arabic (many vowels are excluded from words written in the Arabic alphabet).
All of these earlier works on trigonometry treated it mainly as an adjunct to astronomy; perhaps the first treatment as a subject in its own right was by the De triangulis omnimodus (1464) of Regiomontanus (1436–1476), as well as his later Tabulae directionum (which included the tangent function, unnamed).
The Opus palatinum de triangulis of Rheticus, a student of Copernicus, was the first to define trigonometric functions directly in terms of right triangles instead of circles, with tables for all six trigonometric functions; this work was finished by Rheticus' student Valentin Otho in 1596.
The Introductio in analysin infinitorum (1748) of Euler was primarily responsible for establishing the analytic treatment of trigonometric functions, defining them as infinite series and presenting "Euler's formula" eix = cos(x) + i sin(x). Euler used the near-modern abbreviations sin., cos., tang., cot., sec., and cosec..
References
- Carl B. Boyer, A History of Mathematics, 2nd ed. (Wiley, New York, 1991).
- Eli Maor, Trigonometric Delights (http://www.pupress.princeton.edu/books/maor/) (Princeton Univ. Press, 1998).
- "Trigonometric functions (http://www-gap.dcs.st-and.ac.uk/~history/HistTopics/Trigonometric_functions.html)", MacTutor History of Mathematics Archive.
- Tristan Needham, Visual Complex Analysis, (Oxford University Press, 2000), ISBN 0198534469 Book website (http://www.usfca.edu/vca)
- Vitit Kantabutra, "On hardware for computing exponential and trigonometric functions," IEEE Trans. Computers 45 (3), 328-339 (1996).
See also
- Generating trigonometric tables
- Hyperbolic function
- Pythagoras
- Pythagorean theorem
- Trigonometric identity
- What is trigonometry used for?
External link
- Dave's Short Trig Course (http://babbage.clarku.edu/~djoyce/java/trig/) uses interactive java applets that are very helpful for learning about trig functions on the unit circle, as well as being useful more generally for students of trigonometry.ar:مثلثات
bn:ত্রিকোণমিতি ca:Trigonometria da:Trigonometri de:Trigonometrische Funktion es:Trigonometría eo:Trigonometrio fr:Fonction trigonométrique io:Trigonometriala funciono is:Hornaföll it:Funzioni trigonometriche he:טריגונומטריה nl:Goniometrische functie ja:三角関数 pl:Funkcje trygonometryczne kąta skierowanego pt:Função trigonométrica ru:Тригонометрия sl:Trigonometrična funkcija fi:Trigonometria sv:Trigonometrisk funktion th:ตรีโกณมิติ zh:三角函数