Exponential function
|
|
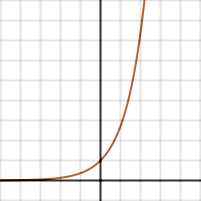
The exponential function is one of the most important functions in mathematics. It is written as exp(x) or ex, where e is the base of the natural logarithm.
As a function of the real variable x, the graph of ex is always positive (above the x axis) and increasing (viewed left-to-right). It never touches the x axis, although it gets arbitrarily close to it (thus, the x axis is a horizontal asymptote to the graph). Its inverse function, the natural logarithm, ln(x), is defined for all positive x.
Sometimes, especially in the sciences, the term exponential function is reserved for functions of the form kax, where a, called the base, is any positive real number. This article will focus initially on the exponential function with base e.
In general, the variable x can be any real or complex number, or even an entirely different kind of mathematical object; see the formal definition below.
| Contents |
Properties
Using the natural logarithm, one can define more general exponential functions. The function
- <math>\!\, a^x=e^{x \ln a}<math>
defined for all a > 0, and all real numbers x, is called the exponential function with base a.
Note that the equation above holds for a = e, since
- <math>\!\, e^{x \ln e}=e^{x\left(1\right)}=e^x.<math>
Exponential functions "translate between addition and multiplication" as is expressed in the following exponential laws:
- <math>\!\, a^0 = 1<math>
- <math>\!\, a^1 = a<math>
- <math>\!\, a^{x + y} = a^x a^y<math>
- <math>\!\, a^{x y} = \left( a^x \right)^y<math>
- <math>\!\, {1 \over a^x} = \left({1 \over a}\right)^x = a^{-x}<math>
- <math>\!\, a^x b^x = (a b)^x<math>
These are valid for all positive real numbers a and b and all real numbers x and y. Expressions involving fractions and roots can often be simplified using exponential notation because:
- <math>{1 \over a} = a^{-1}<math>
and, for any a > 0, real number b, and integer n > 1:
- <math>\sqrt[n]{a^b} = \left(\sqrt[n]{a}\right)^b = a^{b/n}<math>
Derivatives and differential equations
The importance of exponential functions in mathematics and the sciences stems mainly from properties of their derivatives. In particular,
- <math>{d \over dx} e^x = e^x<math>
That is, ex is its own derivative, a property unique among real-valued functions of a real variable. Other ways of saying the same thing include:
- The slope of the graph at any point is the height of the function at that point.
- The rate of increase of the function at x is equal to the value of the function at x.
- The function solves the differential equation y′ = y.
In fact, many differential equations give rise to exponential functions, including the Schrödinger equation and the Laplace's equation as well as the equations for simple harmonic motion.
For exponential functions with other bases:
- <math>{d \over dx} a^x = (\ln a) a^x<math>
Thus any exponential function is a constant multiple of its own derivative.
If a variable's growth or decay rate is proportional to its size — as is the case in unlimited population growth (see Malthusian catastrophe), continuously compounded interest, or radioactive decay — then the variable can be written as a constant times an exponential function of time.
Formal definition
The exponential function ex can be defined in two equivalent ways, as an infinite series:
- <math>e^x = \sum_{n = 0}^{\infty} {x^n \over n!} = 1 + x + {x^2 \over 2!} + {x^3 \over 3!} + {x^4 \over 4!} + \cdots<math>
or as the limit of a sequence:
- <math>e^x = \lim_{n \to \infty} \left( 1 + {x \over n} \right)^n<math> .
In these definitions, <math>n!<math> stands for the factorial of n, and x can be any real number, complex number, element of a Banach algebra (for example, a square matrix), or member of the field of p-adic numbers.
For further explanation of these definitions and a proof of their equivalence, see the article Definitions of the exponential function.
Numerical value
To obtain the numerical value of the exponential function. The infinite series can be rewritten as :
- <math>e^x = {1 \over 0!} + x \, ( {1 \over 1!} + x \, ( {1 \over 2!} + x \, ( {1 \over 3!} + x \, ( {1 \over 4!} + x \, ( {1 \over 5!} + x \, ( {1 \over 6!} + \cdots ))))))<math>
This expression will converge quickly if we can ensure that x is less than one.
To ensure this, we can use the following identity.
- <math>e^x = e^{z+f} = e^z \times [ {1 \over 0!} + f \, ( {1 \over 1!} + f \, ( {1 \over 2!} + f \, ( {1 \over 3!} + f \, ( {1 \over 4!} + f \, ( {1 \over 5!} + f \, ( {1 \over 6!} + \cdots ))))))]<math>
- Where z=int(x)
- Where f = x - z
- Hence, z is an integer value and f is a value less than 1.
The value of the constant e^z can be calculated beforehand by multiplying e with itself z times.
On the complex plane
When considered as a function defined on the complex plane, the exponential function retains the important properties
- <math>\!\, e^{z + w} = e^z e^w<math>
- <math>\!\, e^0 = 1<math>
- <math>\!\, e^z \ne 0<math>
- <math>\!\, {d \over dz} e^z = e^z<math>
for all z and w.
It is a holomorphic function which is periodic with imaginary period <math>2 \pi i<math> and can be written as
- <math>\!\, e^{a + bi} = e^a (\cos b + i \sin b)<math>
where a and b are real values. This formula connects the exponential function with the trigonometric functions and to the hyperbolic functions. Thus we see that all elementary functions except for the polynomials spring from the exponential function in one way or another.
See also Eulers formula in complex analysis Euler's formula.
Extending the natural logarithm to complex arguments yields a multi-valued function, ln(z). We can then define a more general exponentiation:
- <math>\!\, z^w = e^{w \ln z}<math>
for all complex numbers z and w. This is also a multi-valued function. The above stated exponential laws remain true if interpreted properly as statements about multi-valued functions.
The exponential function maps any line in the complex plane to a logarithmic spiral in the complex plane with the center at the origin. This can be seen by noting that the case of a line parallel with the real or imaginary axis maps to a line or circle.
Matrices and Banach algebras
The definition of the exponential function given above can be used verbatim for every Banach algebra, and in particular for square matrices. In this case we have
- <math>e^{x + y} = e^x e^y \mbox{ if } xy = yx<math>
- <math>e^0 = 1<math>
- ex is invertible with inverse e−x
In addition, the derivative of exp at the point x is that linear map which sends u to u · ex.
In the context of non-commutative Banach algebras, such as algebras of matrices or operators on Banach or Hilbert spaces, the exponential function is often considered as a function of a real argument:
- <math>f(t) = e^{t A}<math>
where A is a fixed element of the algebra and t is any real number. This function has the important properties
- <math>f(s + t) = f(s) f(t)<math>
- <math>f(0) = 1<math>
- <math>f'(t) = A f(t)<math>
On Lie algebras
The "exponential map" sending a Lie algebra to the Lie group that gave rise to it shares the above properties, which explains the terminology. In fact, since R is the Lie algebra of the Lie group of all positive real numbers with multiplication, the ordinary exponential function for real arguments is a special case of the Lie algebra situation. Similarly, since the Lie algebra M(n, R) of all square real matrices belongs to the Lie group of all invertible square matrices, the exponential function for square matrices is a special case of the Lie algebra exponential map.
Double exponential function
The term double exponential function can have two meanings:
- a function with two exponential terms, with different exponents
- a function f(x)=a^a^x; this grows even faster than an exponential function; for example, if a=10: f(-1)=1.26, f(0)=10, f(1)=1e10, f(2)=1e100=googol, f(3)=1e1000, ..., f(100)=googolplex.
Compare the super-exponential function, which grows even faster.
See also
External links
Template:Planetmath referenceda:Eksponentialfunktion de:Exponentialfunktion es:Función exponencial fr:Exponentielle he:פונקציה מעריכית ko:지수함수 io:Exponentala ja:指数関数 nl:Exponentiële functie pl:Funkcja wykładnicza pt:Função Exponencial ru:Показательная функция su:Exponential function zh:指数函数