Asymptote
|
|
An asymptote to a curve is a straight line that the curve approaches in such a manner that it becomes as close as one might wish to the line by going far enough along the line. A "real-life" example of such an asymptotic relationship would involve a kitten standing 1m from a box; and, if every hour the kitten walks halfway to the box; this results in a situation in which the kitten never reaches the box; because, the distance it travels, during each hour, is never more than halfway to the box. (Compare Zeno's paradoxes.)
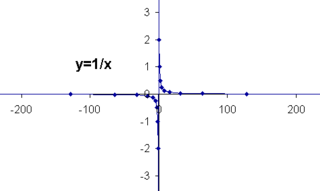
A specific example of asymptotes can be found in the graph of the function f(x) = 1/x, in which two asymptotes are being approached: the line y = 0 and the line x = 0. A curve approaching a vertical asymptote (such as in the preceding example's y = 0, which has an undefined slope) could be said to approach an "infinite limit".
1-over-x-plus-x.png
In the graph of x+x^-1, the y-axis and the line x=y are both asymptotes.
An asymptotes need not be parallel to the x- or y-axis, as shown by the graph of x + x−1, which is asymptotic to both the y-axis and the line y = x. When an asymptote is not parallel to the x- or y-axis, it is called an oblique asymptote.
A function f(x) can be said to be asymptotic to a function g(x) as x → ∞. This has any of four distinct meanings:
- f(x) − g(x) → 0.
- f(x) / g(x) → 1.
- f(x) / g(x) has a nonzero limit.
- f(x) / g(x) is bounded and does not approach zero. See Big O notation.
- See also asymptotic analysis, but contrast with asymptotic curve.
Horizontal asymptotes locator theorem for rational functions
Ask: What is the highest power n of x in the numerator?
What is the highest power d of x in the denominator?
- If n = d, then there is an asymptote at y = leading coefficient of numerator/leading coefficient of denominator
- If n > d Then there is no strictly horizontal asymptote
- If n < d Then the x-axis is a horizontal asymptote.da:Asymptote
de:Asymptote eo:Asimptoto fr:Asymptote nl:Asymptoot pl:Asymptota ru:Асимптота uk:Асимптота zh:渐近线