Distance
|
|
This article is about distance in the mathematical / physical sense. For distance between people, see personal space, proxemics.
The distance between two points is the length of a straight line segment between them. In the case of two locations on Earth, usually the distance along the surface is meant: either "as the crow flies" (along a great circle) or by road, railroad, etc. Distance is sometimes expressed in terms of the time to cover it, for example walking or by car. Sometimes a distance thus indicated is ambiguous because the means of transport is neither mentioned nor obvious.
Distance as mentioned above is sometimes not symmetric, hence not a metric (see below): this applies to distance by car in the case of one-way streets, and also in the case the distance is expressed in terms of the time to cover it (a road may be more crowded in one direction than in the other, for a ship upstream and downstream makes a difference).
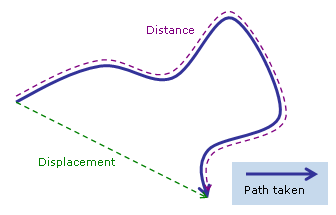
As opposed to a position coordinate, a distance can not be negative. Distance is a scalar quantity, containing only a magnitude, whereas displacement is an equivalent vector quantity containing both magnitude and direction.
| Contents |
Distance covered
The distance covered by a vehicle (often recorded by a odometer), person, animal, object, etc. should be distinguished from the distance from starting point to end point, even if latter is taken to mean e.g. the shortest distance along the road, because a detour could be made, and the end point can even coincide with the starting point.
Formal definition
A distance between two points P and Q in a metric space is d(P,Q), where d is the distance function. We can also define the distance between two sets A and B in a metric space as being the minimum (or infimum) of distances between any two points P in A and Q in B.
The distance formula
The (Euclidean) distance, d, between two points expressed in Cartesian coordinates equals the square root of the sum of the squares of the changes of each coordinate. Thus, in a two-dimensional space
<math>d = \sqrt{(\Delta x)^2 + (\Delta y)^2},<math>
and in a three-dimensional space:
<math>d = \sqrt{(\Delta x)^2 + (\Delta y)^2 + (\Delta z)^2}.<math>
Here, "Δ" (delta) refers to the change in a variable. Thus, Δx is the change in x, pronounced as such, or as "delta-x". In mathematical terms, <math>\Delta x = x_1 - x_0.<math>
This distance formula can be seen as a specialized form of the Pythagorean theorem; it can also be expanded into the arc-length formula.
Generalized distance in arbitrary dimensions: Norms
In the Euclidean space Rn, the distance between two points is usually given by the Euclidean distance (2-norm distance). Other distances, based on other norms, are sometimes used instead. For a point (x1, x2, ...,xn) and a point (y1, y2, ...,yn), the distances are defined as:
| 1-norm distance | <math> = \sum_{i=1}^n \left| x_i - y_i \right|<math> |
| 2-norm distance | <math> = \left( \sum_{i=1}^n \left| x_i - y_i \right|^2 \right)^\frac{1}{2}<math> |
| p-norm distance | <math> = \left( \sum_{i=1}^n \left| x_i - y_i \right|^p \right)^\frac{1}{p}<math> |
| infinity norm distance | <math> = \lim_{p \to \infty} \left( \sum_{i=1}^n \left| x_i - y_i \right|^p \right)^\frac{1}{p}<math> |
| <math> = \max \left(|x_1 - y_1|, |x_2 - y_2|, \ldots |x_n - y_n| \right).<math> |
The 2-norm distance is the Euclidean distance, a generalization of the Pythagorean theorem to more than two coordinates. It is what would be obtained if the distance between two points were measured with a ruler: the "intuitive" idea of distance.
The 1-norm distance is more colourfully called the taxicab norm or Manhattan distance, because it is the distance a car would drive in a city laid out in square blocks (if there are no one-way streets).
If you measure the strength of each of the n links in a chain (where larger numbers mean weaker links), then because a chain is only as strong as its weakest link, the strength of the chain will be the infinity-norm distance from the list of measurements to the origin.
The p-norm is rarely used for values of p other than 1, 2, and infinity, but see super ellipse.
Other norms
- Manhattan distance (taxicab geometry)
- Chebyshev distance represents the distance kings, queens, and bishops must travel between two squares on a chessboard.
Distances in other spaces
- Mahalanobis distance is used in statistics.
- Hamming distance is used in coding theory.
- Levenshtein distance
See also
- astronomical units of length
- cosmic distance ladder
- comoving distance
- distance geometry
- distance-based road exit numbers
- Distance Measuring Equipment (DME)
- great circle distance
- length
- milestone
- neighborhood
- orders of magnitude (length)
- proximity fusede:Abstand
es:Distancia eo:Distanco fr:Distance (mathématiques) ia:Distantia is:Fjarlægðarformúlan ja:距離 nl:Afstand pl:Odległość pt:Distância simple:Distance vi:Khoảng cách zh-cn:距离