Limit of a function
|
|
In mathematics, the limit of a function is a fundamental concept in mathematical analysis.
Rather informally, to say that a function f has limit L at a point p, is to say that the values taken by f get arbitrarily close to L at points close to p. Formal definitions, first devised around the end of the 19th century, are given below.
See net (topology) for a generalization of the concept of limit.
| Contents |
History
Formal definition
Functions on metric spaces
Suppose f : (M,dM) -> (N,dN) is a map between two metric spaces, p∈M and L∈N. We say that "the limit of f at p is L" and write
- <math> \lim_{x \to p}f(x) = L <math>
if and only if for every ε > 0 there exists a δ > 0 such that for all x∈M with dM(x, p) < δ, we have dN(f(x), L) < ε.
Real-valued functions
The real line with metric <math>d(x, y) := |x-y|<math> is a metric space. Also the extended real line with metric <math>d(x, y) := |arctan(x)-arctan(y)|<math> is a metric space.
Limit of a function at a point
Suppose f is a real-valued function, then we write
- <math> \lim_{x \to p}f(x) = L <math>
- for every ε > 0 there exists a δ > 0 such that for all real numbers x with 0 < |x-p| < δ, we have |f(x)-L| < ε
It is just a particular case of functions on metric spaces, with both M and N are the real numbers.
Or we write
- <math> \lim_{x \to p}f(x) = \infty<math>
if and only if
- for every R > 0 there exists a δ > 0 such that for all real numbers x with 0 < |x-p| < δ, we have f(x) > R;
or we write
- <math> \lim_{x \to p}f(x) = -\infty<math>
if and only if
- for every R < 0 there exists a δ > 0 such that for all real numbers x with 0 < |x-p| < δ, we have f(x) < R.
If, in the definitions, x-p is used instead of |x-p|, then we get a right-handed limit, denoted by limx→p+. If p-x is used, we get a left-handed limit, denoted by limx→p-. See main article one-sided limit.
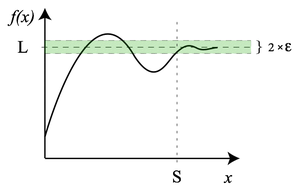
Limit of function at infinity
Suppose f(x) is a real-valued function. We can also consider the limit of function when x increases or decreases indefinitely.
We write
- <math> \lim_{x \to \infty}f(x) = L<math>
if and only if
- for every ε > 0 there exists S >0 such that for all real numbers x>S, we have |f(x)-L|<ε
or we write
- <math> \lim_{x \to \infty}f(x) = \infty<math>
- for every R > 0 there exists S >0 such that for all real numbers x>S, we have f(x)>R.
Similarly, we can define the expressions
- <math> \lim_{x \to \infty}f(x) = -\infty, \lim_{x \to -\infty}f(x) = L, \lim_{x \to -\infty}f(x) = \infty, \lim_{x \to -\infty}f(x) = -\infty<math>.
There are three basic rules for evaluating limits at infinity for a rational function f(x) = p(x)/q(x):
- If the degree of p is greater than the degree of q, then the limit is positive or negative infinity depending on the signs of the leading coefficients
- If the degree of p and q are equal, the limit is the leading coefficient of p divided by the leading coefficient of q
- If the degree of p is less than the degree of q, the limit is 0
If the limit at infinity exists, it represents a horizontal asymptote at x = L. Polynomials do not have horizontal asymptotes; they may occur with rational functions.
Complex-valued functions
The complex plane with metric <math>d(x, y) := |x-y|<math> is also a metric space. There are two different types of limits when we consider complex-valued functions.
Limit of a function at a point
Suppose f is a complex-valued function, then we write
- <math> \lim_{x \to p}f(x) = L <math>
if and only if
- for every ε > 0 there exists a δ >0 such that for all real numbers x with 0<|x-p|<δ, we have |f(x)-L|<ε
It is just a particular case of functions over metric spaces with both M and N are the complex plane.
Limit of a function at infinity
We write
- <math> \lim_{x \to \infty}f(x) = L<math>
if and only if
- for every ε > 0 there exists S >0 such that for all complex numbers |x|>S, we have |f(x)-L|<ε
Examples
Real-valued functions
| <math>\lim_{x \to 3}x^2=9<math> | The limit of x2 as x approaches 3 is 9. In this case, the function happens to be continuous and the value is defined at the point, so the limit is equal to the direct evaluation of the function. |
| <math>\lim_{x \to 0^+}x^x=1<math> | The limit of xx as x approaches 0 from the right is 1. |
| <math>\lim_{x \to 0}{1 \over x} = \mbox{Undefined}<math> <math>\lim_{x \to 0^+}{1 \over x} = +\infty<math> | The two-sided limit of 1/x as x approaches 0 does not exist. The limit of 1/x as x approaches 0 from the right is +∞. |
| <math>\lim_{x \to 0^+}{|x| \over x}=1<math> <math>\lim_{x \to 0^-}{|x| \over x}=-1<math> | The one-sided limit of |x|/x as x approaches 0 is 1 from the positive side and -1 from the negative side. Note that |x|/x = -1 if x is negative and |x|/x = 1 if x is positive. |
| <math>\lim_{x \to 0}x \sin {1 \over x} = 0<math> | The limit of x sin(1/x) as x approaches 0 is 0. |
| <math>\lim_{|x| \to \infty}x^{-a} = 0 \mbox{ if } a \in \mathbb{R}; a>0; x \in \mathbb{C}<math> | Any negative power function approaches 0 as the magnitude of x approaches infinity. |
| <math>\lim_{x \to \infty}{x^a \over b^x} = 0 \mbox{ if } a,b \in \mathbb{R}; b>0<math> | Any power function vanishes in magnitude compared to any increasing exponential function as x approaches infinity. |
| <math>\lim_{x \to \infty}{\log_b x \over x^a} = 0 \mbox{ if } a,b \in \mathbb{R}; a>0; b>0<math> | Any logarithm function vanishes in magnitude compared to any positive power function as x approaches infinity. |
| <math>\lim_{x \to \infty}{a^x \over x!} = 0 \mbox{ if } a \in \mathbb{R}<math> | Any exponential function vanishes in magnitude compared to any factorial function as x approaches infinity. |
Functions on metric spaces
- If z is a complex number with |z| < 1, then the sequence z, z2, z3, ... of complex numbers converges with limit 0. Geometrically, these numbers "spiral into" the origin, following a logarithmic spiral.
- In the metric space C[a,b] of all continuous functions defined on the interval [a,b], with distance arising from the supremum norm, every element can be written as the limit of a sequence of polynomial functions. This is the content of the Stone-Weierstrass theorem.
Properties
To say that the limit of a function f at p is L is equivalent to saying
- for every convergent sequence (xn) in M with limit equal to p, the sequence (f(xn)) converges with limit L.
In the case that f is real-valued, then it is also equivalent to saying that both the right-handed limit or left-handed limit of f at p are L.
The function f is continuous at p if and only if the limit of f(x) as x approaches p exists and is equal to f(p). Equivalently, f transforms every sequence in M which converges towards p into a sequence in N which converges towards f(p).
Again, if N is a normed vector space, then the limit operation is linear in the following sense: if the limit of f(x) as x approaches p is L and the limit of g(x) as x approaches p is P, then the limit of f(x) + g(x) as x approaches p is L + P. If a is a scalar from the base field, then the limit of af(x) as x approaches p is aL.
Taking the limit of functions is compatible with the algebraic operations, provided the limits on the right sides of the identity below exist:
- <math>\begin{matrix}
\lim_{x \to p} & (f(x) + g(x)) & = & \lim_{x \to p} f(x) + \lim_{x \to p} g(x) \\ \lim_{x \to p} & (f(x) - g(x)) & = & \lim_{x \to p} f(x) - \lim_{x \to p} g(x) \\ \lim_{x \to p} & (f(x) g(x)) & = & \lim_{x \to p} f(x) \cdot \lim_{x \to p} g(x) \\ \lim_{x \to p} & (f(x)/g(x)) & = & {\lim_{x \to p} f(x) / \lim_{x \to p} g(x)} \end{matrix}<math>
(the last provided that the denominator is non-zero). In each case above, when the limits on the right do not exist, or, in the last case, when the limits in both the numerator and the denominator are zero, nonetheless the limit on the left may still exist -- this depends on which functions f and g are.
These rules are also valid for one-sided limits, for the case p = ±∞, and also for infinite limits using the rules
- q + ∞ = ∞ for q ≠ -∞
- q × ∞ = ∞ if q > 0
- q × ∞ = −∞ if q < 0
- q / ∞ = 0 if q ≠ ± ∞
(see extended real number line).
Note that there is no general rule for the case q / 0; it all depends on the way 0 is approached. Indeterminate forms, for instance 0/0, 0×∞ ∞-∞ or ∞/∞, are also not covered by these rules but the corresponding limits can often be determined with L'Hôpital's rule.
See also
- How to evaluate the limit of a real-valued function
- Limit of a sequence
- Net (topology)
- Big O notation
References
- Visual Calculus (http://archives.math.utk.edu/visual.calculus/) by Lawrence S. Husch, University of Tennessee (2001)