SO(8)
|
|
In mathematics, SO(8) is the special orthogonal group acting on eight-dimensional Euclidean space. It could be either a real or complex simple Lie group of rank 4 and dimension 28. Like all special orthogonal groups, SO(8) is not simply connected having a fundamental group isomorphic to Z2. The universal cover of SO(8) is the spinor group Spin(8). The center of Spin(8) is Z2×Z2 while the center of SO(8) is Z2.
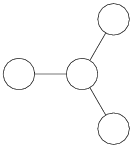
SO(8) is unique among the simple Lie groups in that its Dynkin diagram (shown right) (D4 under the Dynkin classification) possesses a high degree of symmetry. This gives rise to peculiar feature of Spin(8) known as triality. Related to this is the fact that the two spinor representations, as well as the fundamental vector representation, of Spin(8) are all eight-dimensional (In all other dimensions the spinor representation is either smaller or larger than the vector representation). The triality automorphism of Spin(8) is the outer automorphism group of Spin(8) which is isomorphic to the symmetric group S3 that permutes these three representations. By contrast, the outer automorphism group of SO(8) (i.e. Spin(8)/Z2) is only Z2.
In other words, spin(8) can be "enlarged" to the semidirect product spin(8) S3.
S3.
Root system
<math>(\pm 1,\pm 1,0,0)<math>
<math>(\pm 1,0,\pm 1,0)<math>
<math>(\pm 1,0,0,\pm 1)<math>
<math>(0,\pm 1,\pm 1,0)<math>
<math>(0,\pm 1,0,\pm 1)<math>
<math>(0,0,\pm 1,\pm 1)<math>
Weyl group
Its Weyl/Coxeter group has 4!×8=192 elements.
Cartan matrix
<math> \begin{pmatrix} 2 & -1 & -1 & -1\\ -1 & 2 & 0 & 0\\ -1 & 0 & 2 & 0\\ -1 & 0 & 0 & 2 \end{pmatrix} <math>
See also: Octonions, Clifford algebra, G2