G2 (mathematics)
|
|
In mathematics, G2 is the name of a Lie group and also its Lie algebra <math>\mathfrak{g}_2<math>. It is the smallest of the five exceptional simple Lie groups. G2 has rank 2 and dimension 14. Its center is the trivial subgroup. Its outer automorphism group is the trivial group. Its fundamental representation is 7-dimensional.
G2 can be described as the automorphism group of the octonion algebra or, equivalently, as the subgroup of <math>SO(7)<math> that preserves any chosen particular vector in its 8-dimensional real spinor representation.
| Contents |
Algebra
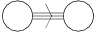
Dynkin diagram
Roots of G2
Although they span a 2-dimensional space, it's much more symmetric to consider them as vectors in a 2-dimensional subspace of a three dimensional space.
- (1,−1,0),(−1,1,0)
- (1,0,−1),(−1,0,1)
- (0,1,−1),(0,−1,1)
- (2,−1,−1),(−2,1,1)
- (1,−2,1),(−1,2,−1)
- (1,1,2),(−1,−1,2)
Simple roots
- (0,1,−1), (1,−2,1)
Weyl/Coxeter group
Its Weyl/Coxeter group is the dihedral group, D6.
Cartan matrix
- <math>
\begin{pmatrix} 2&-3\\ -1&2 \end{pmatrix} <math>
Special holonomy
G2 is one of the possible special groups that can appear as holonomy. The manifolds of G2 holonomy are also called Joyce manifolds.
| E6 | E7 | E8 | F4 | G2 |