Dihedral group
|
|
In mathematics, the dihedral group Dn is a certain nonabelian group of order 2n. It is usually thought of a group of transformations of the Euclidean plane consisting of rotations (about the origin) and reflections (across lines through the origin). As such it is the symmetry group of a regular polygon with n sides (for n > 2).
Warning: Many authors use the notation D2n instead of Dn for the dihedral group of order 2n.
Specifically the dihedral group Dn is generated by a rotation r of order n and a reflection f of order 2 such that
- <math>frf = r^{-1}.<math>
One specific matrix representation is given by
- <math>r = \begin{bmatrix}\cos{2\pi \over n} & -\sin{2\pi \over n} \\ \sin{2\pi \over n} & \cos{2\pi \over n}\end{bmatrix} \qquad f = \begin{bmatrix}1 & 0 \\ 0 & -1\end{bmatrix}<math>
The simplest dihedral group is D2, which is generated by the rotation r of 180 degrees, and the reflection f across the y-axis. The elements of D2 can then be represented as {e, r, f, rf}, where e is the identity or null transformation and rf is the reflection across the x-axis.
Missing image
Dihedral4.png
image:dihedral4.png
D2 is isomorphic to the Klein four-group.
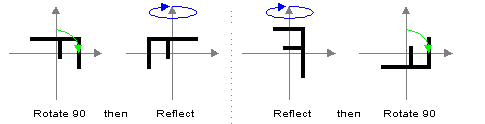
If the order of Dn is greater than 4, the operations of rotation and reflection in general do not commute and Dn is not abelian; for example, in D4, a rotation of 90 degrees followed by a reflection yields a different result from a reflection followed by a rotation of 90 degrees:
Thus, beyond their obvious application to problems of symmetry in the plane, these groups are among the simplest examples of non-abelian groups, and as such arise frequently as easy counterexamples to theorems which are restricted to abelian groups.
The 2n elements of Dn can be written as e, r, r2,...,rn−1, f, fr, fr2,...,frn−1. The first n listed elements are rotations and the remaining n elements are axis-reflections (all of which have order 2). The product of two rotations or two reflections is a rotation; the product of a rotation and a reflection is a reflection.
So far, we have considered Dn to be a subgroup of O(2), i.e. the group of rotations (about the origin) and reflections (across axes through the origin) of the plane. One can also think of Dn as a subgroup of SO(3), i.e. the group of rotations (about the origin) of the three-dimensional space. From this point of view, Dn is the proper symmetry group of a regular polygon embedded in three-dimensional space (if n ≥ 3). Such a figure may be considered as a degenerate regular solid with its face counted twice. Therefore it is also called a dihedron (Greek: solid with two faces), which explains the name dihedral group (in analogy to tetrahedral, octahedral and icosahedral group, referring to the proper symmetry groups of a regular tetrahedron, octahedron, and icosahedron respectively).
Further equivalent definitions of Dn are:
- The automorphism group of the graph consisting only of a cycle with n vertices (if n ≥ 3).
- The group with presentation
- <math>\langle r, f \mid r^n = 1, f^2 = 1, frf = r^{-1} \rangle<math>
- or
- <math>\langle x, y \mid x^2 = y^2 = (xy)^n = 1 \rangle<math>
- (Indeed the only finite groups that can be generated by two elements of order 2 are the dihedral groups and the cyclic groups)
- The semidirect product of cyclic groups Cn and C2, with C2 acting on Cn by inversion (thus, Dn always has a normal subgroup isomorphic to Cn)
If we consider Dn (n ≥ 3) as the symmetry group of a regular n-gon and number the polygon's vertices, we see that Dn is a subgroup of the symmetric group Sn.
The properties of the dihedral groups Dn with n ≥ 3 depend on whether n is even or odd. For example, the center of Dn consists only of the identity if n is odd, but contains the element rn/2 if n is even. All the reflections are conjugate to each other in case n is odd, but they fall into two conjugacy classes if n is even. This corresponds to the geometrical fact that every symmetry axis of a regular n-gon passes through a vertex and an opposite side if n is odd, but half of them pass through opposite sides and half pass through opposite vertices if n is even.
If m divides n, then Dm is a subgroup of Dn. The total number of subgroups of Dn (n ≥ 3), is equal to d(n) + σ(n), where d(n) is the number of positive divisors of n and σ(n) is the sum of the positive divisors of n.
Generalizations
In addition to the finite dihedral groups, there is the infinite dihedral group D∞. Every dihedral group is generated by a rotation r and a reflection; if the rotation is a rational multiple of a full rotation, then there is some integer n such that rn is the identity, and we have a finite dihedral group. If the rotation is not a rational multiple of a full rotation, then there is no such n and the resulting group has infinitely many elements and is called D∞. It has presentations
- <math>\langle r, f \mid f^2 = 1, frf = r^{-1} \rangle<math>
- <math>\langle x, y \mid x^2 = y^2 = 1 \rangle<math>
and is isomorphic to a semidirect product of Z and C2, and to the free product C2 * C2. It can also be visualized as the automorphism group of the graph consisting of a path infinite to both sides.
Finally, if H is any abelian group, we can speak of the generalized dihedral group of H (sometimes written Dih(H)). This group is a semidirect product of H and C2, with C2 acting on H by inverting elements. Dih(H) has a normal subgroup of index 2 isomorphic to H, and contains in addition an element f of order 2 such that, for all x in H, x f = f x −1. Clearly, we have Dn = Dih(Cn) and D∞ = Dih(Z). The symmetry group of a straight line is isomorphic to Dih(R) and the symmetry group of a circle is Dih(S1) (where S1 denotes the multiplicative group of complex numbers of absolute value 1).