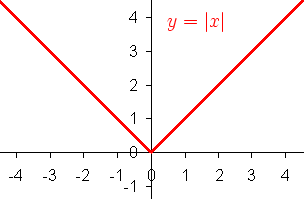
Absolute value
|
|
In mathematics, the absolute value (or modulus) of a real number is its numerical value without regard to its sign. So, for example, 3 is the absolute value of both 3 and −3, and 0 is the only absolute value of 0.
| Contents |
Definition
It can be defined as follows: For any real number a, the absolute value of a, denoted |a|, is equal to a if a ≥ 0, and to −a, if a < 0 (see also: inequality). |a| is never negative, as absolute values are always either positive or zero. Put another way, |a| < 0 has no solution for a. Also, it is not necessary that |-a| = a since a can be negative.
The absolute value can be regarded as the distance of a number from zero; indeed the notion of distance in mathematics is a generalisation of the properties of the absolute value. When real numbers are considered as one-dimensional vectors, the absolute value is the magnitude, and the p-norm for any p. Up to a constant factor, every norm in R1 is equal to the absolute value: ||x||=||1||.|x|
Properties
The absolute value has the following properties:
- |a| ≥ 0
- |a| = 0 iff a = 0.
- |ab| = |a||b|
- |a/b| = |a| / |b| (if b ≠ 0)
- |a+b| ≤ |a| + |b| (the triangle inequality)
- |a−b| ≥ ||a| − |b||
- <math>\left| a \right| = \sqrt{a^2}<math>
- |a| ≤ b iff −b ≤ a ≤ b
- |a| ≥ b iff a ≤ −b or b ≤ a
The last two properties are often used in solving inequalities; for example:
- |x − 3| ≤ 9
- −9 ≤ x−3 ≤ 9
- −6 ≤ x ≤ 12
For real arguments, the absolute value function f(x) = |x| is continuous everywhere and differentiable everywhere except for x = 0. For complex arguments, the function is continuous everywhere but differentiable nowhere (One way to see this is to show that it does not obey the Cauchy-Riemann equations).
For a complex number z = a + ib, one defines the absolute value or modulus to be |z| = √(a2 + b2) = √ (z z*) (see square root and complex conjugate). This notion of absolute value shares the properties 1-6 from above. If one interprets z as a point in the plane, then |z| is the distance of z to the origin.
It is useful to think of the expression |x − y| as the distance between the two numbers x and y (on the real number line if x and y are real, and in the complex plane if x and y are complex). By using this notion of distance, both the set of real numbers and the set of complex numbers become metric spaces.
The function is not invertible, because a negative and a positive number have the same absolute value.
Absolute value of complex numbers
The absolute value, also called modulus, of a complex number <math>c\in\mathbb C<math> is given by <math>|c| = \sqrt{c\,\overline c}<math>, where <math>\overline c<math> is its complex conjugate. Writing <math>c = a + b\,i<math> with <math>a, b\in\mathbb R<math>, this becomes <math>|c| = \sqrt{a^2 + b^2}<math>.
Like the absolute value of real numbers, this is a special case of the norm in an inner product space. It is identical to the Euclidean norm, if the complex plane is identified with the Euclidean plane R2.
Absolute value of vectors
The absolute value of a vector v, (x1, x2,..., xn), is given by
Note that |v| is also the length of the vector v.
Algorithm
In the C programming language, the abs(), labs(), llabs() (in C99), fabs(), fabsf(), and fabsl() functions compute the absolute value of an operand. Coding the integer version of the function is trivial, ignoring the boundary case where the largest negative integer is input:
int abs(int i)
{
if (i < 0)
return -i;
else
return i;
}
The floating-point versions are trickier, as they have to contend with special codes for infinity and not-a-numbers.
Using assembly language, it is possible to take the absolute value of a register in just three instructions (example shown for a 32-bit register on an x86 architecture, Intel syntax):
cdq xor eax, edx sub eax, edx
cdq extends the sign bit of eax into edx. If eax is nonnegative, then edx becomes zero, and the latter two instructions have no effect, leaving eax unchanged. If eax is negative, then edx becomes 0xFFFFFFFF, or -1. The next two instructions then become a two's complement inversion, giving the absolute value of the negative value in eax.de:Absoluter Betrag
es:Valor absoluto
fi:Itseisarvo
fr:Valeur absolue
gl:Valor absoluto
is:Algildi
it:Valore assoluto
he:ערך מוחלט
nl:Absolute waarde
ja:絶対値
pl:Wartość bezwzględna
ru:Абсолютная величина
sl:Absolutna vrednost
sv:Absolutbelopp
zh:绝对值
th:ค่าสัมบูรณ์
sr:Апсолутна вредност