Simple Lie group
|
|
In mathematics, a simple Lie group is a Lie group which is also a simple group. These groups, and groups closely related to them, include many of the so-called classical groups of geometry, which lie behind projective geometry and other geometries derived from it by the Erlangen programme of Felix Klein. They also include some exceptional groups, that were first discovered by those pursuing the classification of simple Lie groups. The exceptional groups account for many special examples and configurations in other branches of mathematics. In particular the classification of finite simple groups depended on a thorough prior knowledge of the 'exceptional' possibilities.
The complete listing of the simple Lie groups is the basis for the theory of the semisimple Lie groups and reductive groups, and their representation theory. This has turned out not only to be a major extension of the theory of compact Lie groups (and their representation theory), but to be of basic significance in particle physics.
| Contents |
Method of classification
Such groups are classified using the prior classification of the complex simple Lie algebras: for which see the page on root systems. It is shown that a simple Lie group has a simple Lie algebra that will occur on the list given there, once it is complexified (that is, made into a complex vector space rather than a real one). This reduces the classification to two further matters.
Real forms
The groups SO(p,q,R) and SO(p+q,R), for example, give rise to different real Lie algebras, but having the same Dynkin diagram. In general there may be different real forms of the same complex Lie algebra.
Relationship of simple Lie algebras to groups
Secondly the Lie algebra only determines uniquely the simply connected (universal) cover G* of the component containing the identity of a Lie group G. It may well happen that G* isn't actually a simple group, for example having a non-trivial center. We have therefore to worry about the global topology, by computing the fundamental group of G (an abelian group: a Lie group is an H-space). This was done by Cartan.
For an example, take the special orthogonal groups in even dimension. With −I a scalar matrix in the center, these aren't actually simple groups; and having a two-fold spin cover, they aren't simply-connected either. They lie 'between' G* and G, in the notation above.
Classification by Dynkin diagram
See main article root system
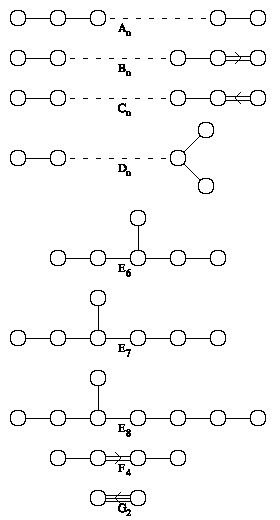
According to Dynkin's classification, we have as possibilities these only, where n is the number of nodes:
Infinite series
A series
A1, A2, ...
Ar corresponds to the special unitary group, SU(r+1).
B series
B1, B2, ...
Br corresponds to the special orthogonal group, SO(2r+1).
C series
C1, C2, ...
Cr corresponds to the symplectic group, Sp(2r).
D series
D2, D3, ...
Dr corresponds to the special orthogonal group, SO(2r). Note that SO(4) is not a simple group, though. The Dynkin diagram has two nodes that are not connected. There is a surjective homomorphism from SO(3)* × SO(3)* to SO(4) given by quaternion multiplication; see quaternions and spatial rotation. Therefore the simple groups here start with D3, which as a diagram straightens out to A3. With D4 there is an 'exotic' symmetry of the diagram, corresponding to so-called triality.
Exceptional algebras
G2
See G2.
F4
See F4.
E6
See E6.
E7
See E7.
E8
See E8.