Root system
|
|
In mathematics, a root system is a configuration of vectors in a Euclidean space satisfying certain geometrical properties. The concept is fundamental in Lie group theory. Since Lie groups (and some analogues such as algebraic groups) became used in most parts of mathematics during the twentieth century, the apparently special nature of root systems belies the number of areas in which they are applied. Further, the classification scheme for root systems, by Dynkin diagrams, occurs in parts of mathematics with no overt connection to Lie groups (such as singularity theory).
| Contents |
Definitions
Let V be a finite-dimensional Euclidean space, with the standard Euclidean inner product denoted by (·,·). A root system in V is a finite set Φ of non-zero vectors (called roots) which satisfy the following properties:
Integrality-of-root-system.png
- The roots span V
- The only scalar multiples of a root α ∈ Φ which belong to Φ are α itself and −α.
- For every root α ∈ Φ, the set Φ is closed under reflection through the hyperplane perpendicular to α. That is, for any two roots α and β,
- <math>\sigma_\alpha(\beta) =\beta-2\frac{(\alpha,\beta)}{(\alpha,\alpha)}\alpha \in \Phi.<math>
- (Integrality condition) If α and β are roots in Φ, then the projection of β onto the line through α is a half-integral multiple of α. That is,
- <math> \langle \beta, \alpha \rangle = 2 \frac{(\alpha,\beta)}{(\alpha,\alpha)} \in \mathbb{Z}, <math>
In view of axiom 3, the integrality condition is equivalent to stating that β and its reflection σα(β) differ be a integer multiple of α. Note that operator
- <math> \langle \cdot, \cdot \rangle \colon \Phi \times \Phi \to \mathbb{Z}<math>
defined by axiom 4 is not an inner product. It is not necessarily symmetric and is linear only in the first argument.
The rank of a root system Φ is the dimension of V. Two root systems may be combined by regarding the Euclidean spaces they span as mutually orthogonal subspaces of a common Euclidean space. A root system which does not arise from such a combination, such as the systems A2, B2, and G2 pictured below, is said to be irreducible.
Two irreducible root systems (E1,Φ1) and (E2,Φ2) are considered to be the same if there is an invertible linear transformation E1→E2 which preserves distance up to a scale factor and which sends Φ1 to Φ2.
The group of isometries of V generated by reflections through hyperplanes associated to the roots of Φ is called the Weyl group of Φ. As it acts faithfully on the finite set Φ, the Weyl group is always finite.
Classification
There is only one root system with rank one consisting of two nonzero vectors {α, −α}. This root system is called A1. In rank 2 there are four possibilities:
| Missing image Root-system-A1xA1.png Root system A1×A1 | Missing image Root-system-A2-v1.png Root system A2 |
| Root system A1×A1 | Root system A2 |
| Missing image Root-system-B2.png Root system B2 | Missing image Root-system-G2.png Root system G2 |
| Root system B2 | Root system G2 |
Whenever Φ is a root system in V and W is a subspace of V spanned by Ψ=Φ∩W, then Ψ is a root system in W. Thus, our exhaustive list of root systems of rank 2 shows the geometric possibilities for any two roots in a root system. In particular, two such roots meet at an angle of 0, 30, 45, 60, 90, 120, 135, 150, or 180 degrees.
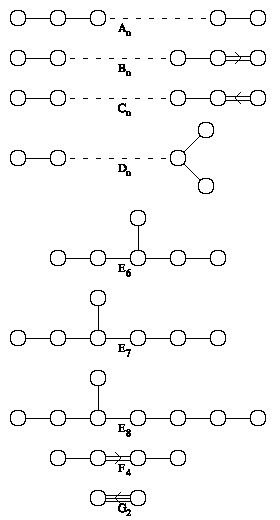
In general, irreducible root systems are specified by a family (indicated by a letter A to G) and the rank (indicated by a subscript). There are four infinite families and five exceptional cases:
Dynkin diagrams
To prove this classification theorem, one uses the angles between pairs of roots to encode the root system in a much simpler combinatorial object, the Dynkin diagram, named for Eugene Dynkin. The Dynkin diagrams can then be classified according to the scheme given above.
To every root system is associated a graph (possibly with a specially marked edge) called the Dynkin diagram which is unique up to isomorphism. The Dynkin diagram can be extracted from the root system by choosing a base, that is a subset Δ of Φ which is a basis of V with the special property that every vector in Φ when written in the basis Δ has either all coefficients ≥0 or else all ≤0. The elements of this base are called simple roots.
The vertices of the Dynkin diagram correspond to vectors in Δ. An edge is drawn between each non-orthogonal pair of vectors; it is an undirected single edge if they make an angle of 120 degrees, a directed double edge if they make an angle of 135 degrees, and a directed triple edge if they make an angle of 150 degrees. In addition, double and triple edges are marked with an angle sign pointing toward the shorter vector.
Although a given root system has more than one base, the Weyl group acts transitively on the set of bases. Therefore, the root system determines the Dynkin diagram. Given two root systems with the same Dynkin diagram, we can match up roots, starting with the roots in the base, and show that the systems are in fact the same.
Thus the problem of classifying root systems reduces to the problem of classifying possible Dynkin diagrams, and the problem of classifying irreducible root systems reduces to the problem of classifying connected Dynkin diagrams. Dynkin diagrams encode the inner product on E in terms of the basis Δ, and the condition that this inner product must be positive definite turns out to be all that is needed to get the desired classification. The actual connected diagrams are as follows:
List of irreducible root systems
The following table lists some properties of the irreducible root systems. Explicit constructions of these systems are given in the following subsections.
| <math>\Phi<math> | <math>|\Phi|<math> | <math>|\Phi^{<}|<math> | I | <math>|W|<math> |
|---|---|---|---|---|
| An | n(n+1) | n+1 | (n+1)! | |
| Bn | 2n2 | 2n | 2 | 2n n! |
| Cn | 2n2 | 2n(n−1) | 2 | 2n n! |
| Dn | 2n(n−1) | 4 | 2n−1 n! | |
| E6 | 72 | 3 | 51840 | |
| E7 | 126 | 2 | 2903040 | |
| E8 | 240 | 1 | 696729600 | |
| F4 | 48 | 24 | 1 | 1152 |
| G2 | 12 | 6 | 1 | 12 |
Here <math>|\Phi^{<}|<math> denotes then number of short roots (if all roots have the same length they are taken to be long by definition), I denotes the determinant of the Cartan matrix, and <math>|W|<math> denotes the order of the Weyl group, i.e. the number of symmetries of the root system.
An
Let V be the subspace of Rn+1 for which the coordinates sum to 0, and let Φ be the set of vectors in V of length √2 and with integer coordinates in Rn+1. Such a vector must have all but two coordinates equal to 0, one coordinate equal to 1, and one equal to −1, so there are n2 + n roots in all.
Bn
Let V=Rn, and let Φ consist of all integer vectors in V of length 1 or √2. The total number of roots is 2n2.
Cn
Let V=Rn, and let Φ consist of all integer vectors in V of √2 together with all vectors of the form 2λ, where λ is an integer vector of length 1. The total number of roots is 2n2.
Dn
Let V=Rn, and let Φ consist of all integer vectors in V of length √2. The total number of roots is 2n(n−1).
En
For V8, let V=R8, and let E8 denote the set of vectors α of length √2 such that the coordinates of 2α are all integers and are either all even or all odd and the sum of all 8 coordinates is even. Then E7 can be constructed as the intersection of E8 with the hyperplane of vectors perpendicular to a fixed root α in E8, and E6 can be constructed as the intersection of E8 with two such hyperplanes corresponding to roots α and β which are neither orthogonal to one another nor scalar multiples of one another. The root systems E6, E7, and E8 have 72, 126, and 240 roots respectively.
F4
For F4, let V=R4, and let Φ denote the set of vectors α of length 1 or √2 such that the coordinates of 2α are all integers and are either all even or all odd. There are 48 roots in this system.
G2
There are 12 roots in G2, which form the vertices of a hexagram. See the picture above.
Root systems and Lie theory
Irreducible root systems classify a number of related objects in Lie theory, notably:
- Simple complex Lie algebras
- Simple complex Lie groups
- Simply connected complex Lie groups which are simple modulo centers
- Simple compact Lie groups
In each case, the roots are non-zero weights of the adjoint representation.