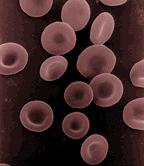
Red blood cell
|
|
Red blood cells are the most common type of blood cell and are the vertebrate body's principal means of delivering oxygen to body tissues via the blood. Red blood cells are also known as RBCs or erythrocytes (from Greek erythros for "red" and kytos for "hollow", nowadays translated as "cell"). A schistocyte is a red blood cell undergoing fragmentation, or a fragmented part of a red blood cell.
Erythrocytes deliver oxygen via hemoglobin, a complex molecule containing heme groups whose iron molecules temporarily link to oxygen molecules in the lungs or gills and release them throughout the body. Hemoglobin also carries some of the waste product carbon dioxide back from the tissues. (Less than 2% of the total oxygen, and most of the carbon dioxide are also held in solution in the blood plasma). Red blood cells consist of almost 90% hemoglobin; the heme is what gives blood its color. A related compound, myoglobin, acts to store oxygen in muscle cells.
| Contents |
Mammalian erythrocytes
Erythrocytes in mammals are anucleate when mature, meaning that they don't have a cell nucleus and thus no DNA. (The erythrocytes of all other vertebrates have nuclei.) Erythrocytes also lose their mitochondria and produce energy by fermentation, via glycolysis of glucose followed by lactic acid production. Red cells lack the insulin receptor and thus glucose uptake is not regulated by insulin.
Mammalian erythrocytes have a biconcave shape: flattened ovate and depressed in the center. This shape is optimized for the exchange of oxygen with the surroundings. The cells are flexible so as to fit through tiny capillaries, where they release their oxygen load.
The spleen acts as a reservoir of red blood cells, but this effect is somewhat limited in humans. In some other mammals such as dogs and horses, the spleen sequesters large numbers of red blood cells that are dumped into the blood during times of exertion stress, yielding a higher oxygen transport capacity.
Human erythrocytes
The diameter of a typical human erythrocyte is 6-8 µm. Adult humans have roughly 2-3 × 1013 red blood cells at any given time (women have about 4-5 million erythrocytes per cubic millimeter (microliter) of blood and men about 5-6 million; people living at high altitudes with low oxygen concentration will have more). Red blood cells are thus much more common than the other blood particles: there are about 4-11 thousand white blood cells and about 150-400 thousand platelets in a cubic millimeter of human blood. The red blood cells store collectively about 3.5 grams of iron; that's more than five times the iron stored by all the other tissues combined.
The blood types of humans are due to variations in surface glycoproteins of erythrocytes.
The process by which red blood cells are produced is called erythropoiesis. Erythrocytes are continuously being produced in the red bone marrow of large bones. (In the embryo, the liver is the main site of red blood cell production.) The production can be stimulated by the hormone erythropoietin (EPO), which is used for doping in sports. Erythrocytes develop in about 7 days and live a total of about 120 days. The aging cells swell up to a sphere-like shape and are engulfed by phagocytes, destroyed and their materials are released into the blood. The main sites of destruction are the liver and the spleen. The heme constituent of hemoglobin is eventually excreted as bilirubin.
Red blood cells can be separated from blood plasma by centrifugation. During plasma donation, the red blood cells are pumped back into the body right away, and the plasma is collected. Some athletes have tried to improve their performance by doping their blood: first about 1 liter of their blood is extracted, then the red blood cells are isolated, frozen and stored, to be reinjected shortly before the competition. (Red blood cells can be conserved for 5 weeks at -78° Celsius.) This practice is hard to detect but may endanger the human cardiovascular system because it is not equipped to deal with blood of the resulting higher viscosity.
Diseases and diagnostic tools
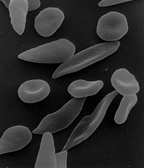
Blood diseases involving the red blood cells include:
- Anemias (or anaemias) are diseases characterized by low oxygen transport capacity of the blood, because of low red cell count or some abnormality of the red blood cells or the hemoglobin.
- Iron deficiency anemia is the most common anemia; it occurs when the dietary intake or absorption of iron is insufficient, and hemoglobin, which contains iron, cannot be formed
- Sickle-cell anemia is a genetic disease which leads to mis-shaped red blood cells.
- Thalassemia is a genetic disease that results in the production of abnormal hemoglobin molecules.
- Spherocytosis is a genetic disease that causes a defect in the red blood cell's cytoskeleton, causing the RBCs to be small, sphere-shaped, and fragile instead of donut-shaped and flexible.
- Pernicious anemia is an autoimmune disease where the body lacks intrinsic factor, required to absorb vitamin B12 from food. Vitamin B12 is needed for the production of hemoglobin.
- Aplastic anemia is caused by the inability of the bone marrow to produce blood cells.
- The malaria parasite spends part of its life-cycle in red blood cells and feeds on hemoglobin. Both sickle-cell anemia and thalassemia are more common in malaria areas, because these mutations convey some protection against the parasite.
- Polycythemias (or erythrocytoses) are diseases characterized by a surplus of red blood cells. The increased viscosity of the blood can cause a number of symptoms.
- In polycythemia vera the increased number of red blood cells results from an abnormality in the bone marrow.
Several blood tests involve red blood cells, including the RBC count (the number of red blood cells per volume of blood) and the hematocrit (percentage of blood volume occupied by red blood cells). The blood type needs to be determined to prepare for a blood transfusion or an organ transplantation.
History
In 1658, the Dutch Jan Swammerdam was the first to describe red blood cells; he had used an early microscope.
| Cardiovascular system - Blood |
| Red blood cells - White blood cells - Platelets - Blood plasma |
| White blood cells |
| Granulocytes (Neutrophil granulocytes, Eosinophil granulocytes, Basophil granulocytes) - Lymphocytes - Monocytes |
| Coagulation |
| Coagulation factors: - Fibrin (I) - (Pro)thrombin (II) - FV - FVII - FVIII - FIX - FX - FXI - FXII - FXIII - HMWK - vWF - Tissue factor |
| Inhibitors: Antithrombin - Protein C - Protein S - Protein Z - ZPI - TFPI |
| Fibrinolysis: Plasmin - tPA/urokinase - PAI-1/2 - α2-AP - TAFI |
es:Eritrocito eo:Eritrocito fr:Hématie ko:적혈구 ia:Erythrocyto it:Globulo rosso nl:Rode bloedcel ja:赤血球 pl:Erytrocyt fi:Punasolu ta:இரத்தச் சிவப்பணு zh:红血球