Parallax
|
|
- This article is about parallax, the perspective shift. For the DC comic book character see Parallax (comics).
Parallax (Greek: παραλλαγή (parallagé) = alteration) is the change of angular position of two stationary points relative to each other as seen by an observer, due to the motion of said observer. Or more simply put, it is the apparent shift of an object against a background due to a change in observer position.
| Contents |
Informal introduction
Parallax_Example.png
Parallax is often thought of as the "apparent motion" of an object against a distant background because of a perspective shift, as seen in Figure 1. When viewed from Viewpoint A, the object appears to be in front of the blue square. When the viewpoint is changed to Viewpoint B, the object appears to have moved to in front of the red square.
Use in distance measurement
By observing parallax, measuring angles, and using geometry; one can determine the distance to various objects. When this is in reference to stars, the effect is known as stellar parallax. The first measurements of a stellar parallax were made by Friedrich Bessel in 1838.
Distance measurement by parallax is a special case of the principle of triangulation, where one can solve for all the sides and angles in a network of triangles if, in addition to all the angles in the network, the length of only one side has been measured. Thus, the careful measurement of the length of one baseline can fix the scale of a triangulation network covering the whole nation. In parallax, the triangle is extremely long and narrow, and by measuring both its shortest side and the small top angle (the other two being close to 90 degrees), the long sides (in practice equal) can be determined.
Parallax of the human eye
With a nearby object in front of you, gaze at infinity. Cover one eye with your hand. Then move your hand to cover your other eye instead. The nearby object will seem to jump horizontally.
It is this effect that allows us — and certain other animals such as cats — to see depth. It is used in simple stereo viewing devices, such as the Viewmaster™ used to view stereoscopic scenery in the form of two images taken from adjacent locations. The Apollo astronauts on the Moon knew how to take such stereo pairs, clicking two frames of the same object in locations shifted slightly horizontally with respect to each other.
A way to allow a crowd of people simultaneously to view a stereoscopic scene is to provide them with anaglyph glasses. One glass is red, the other green or blue, and the stereo scene is produced by the printing process in a corresponding fashion. It is generally believed that such scenes are of necessity monochrome — red for the left image, green\blue for the right — but this is not quite true: working colour anaglyphic scenes have been produced.
Instructions for self-producing anaglyphic glasses by copying colour onto an overhead projector sheet can be easily obtained. Better quality glasses can also be purchased inexpensively from many science shops or internet mail orders.
Autostereograms exploit the effect of parallax to allow viewers to see 3D shapes in a single 2D image.
Parallax and measurement instruments
If an optical instrument — telescope, microscope, theodolite — is imprecisely focused, the cross-hairs will appear to move with respect to the object focused on if one moves one's head horizontally in front of the eyepiece. This is why it is important, especially when performing measurements, to carefully focus in order to 'eliminate the parallax', and to check by moving one's head.
Also in non-optical measurements, e.g., the thickness of a ruler can create parallax in fine measurements. One is always cautioned in science classes to "avoid parallax." By this it is meant that one should always take measurements with one's eye on a line directly perpendicular to the ruler, so that the thickness of the ruler does not create error in positioning for fine measurements. A similar error can occur when reading the position of a pointer against a scale in an instrument such as a galvanometer. To help the user to avoid this problem, the scale is sometimes printed above a narrow strip of mirror, and the user positions his eye so that the pointer obscures its own reflection. This guarantees that the user's line of sight is perpendicular to the mirror and therefore to the scale.
In photography, one also talks about the parallax of a camera viewfinder: for nearby objects, a viewfinder mounted on top of the camera will show something different from what the lens 'sees', and people's heads may be cut off. The problem does not exist for the single lens reflex camera, where the viewfinder looks (with the aid of a movable mirror) through the same lens as is used for taking the photograph.
Photogrammetric parallax
Aerial photograph pairs, when viewed through a stereo viewer, offer a spectacular stereo effect of landscape and buildings. High buildings appear to 'keel over' in the direction away from the centre of the photograph. Measuring this effect, also called parallax, allows one, if the flying height and the distance between the aircraft's exposure locations is known, to deduce the building's height.
Lunar parallax
Jules Verne, From the Earth to the Moon (1865). "Up till then, many people had no idea how one could calculate the distance separating the Moon from the Earth. The circumstance was exploited to teach them that this distance was obtained by measuring the parallax of the Moon. If the word parallax appeared to amaze them, they were told that it was the angle subtended by two straight lines running from both ends of the Earth's radius to the Moon. If they had doubts on the perfection of this method, they were immediately shown that not only did this mean distance amount to a whole two hundred thirty-four thousand three hundred and forty-seven miles (94,330 leagues), but also that the astronomers were not in error by more than seventy miles (— 30 leagues)."
A primitive way to determine the lunar parallax from one location is by using a lunar eclipse. The full shadow of the Earth on the Moon has an apparent radius of curvature equal to the difference between the apparent radii of the Earth and the Sun as seen from the Moon. This radius can be seen to be equal to 0.75 degree, from which (with the solar apparent radius 0.25 degree) we get an Earth apparent radius of 1 degree. This yields for the Earth-Moon distance 60 Earth radii or 384,000 km.
Another way to use parallax to determine the distance to the Moon would be to take two pictures of the Moon at exactly the same time from two locations on Earth, and compare the position of the Moon relative to the visible stars. Using the orientation of the Earth, and those two points, and a perpendicular displacement, a distance to the Moon can be triangulated.
- <math>distance_{moon} = \frac {distance_{observerbase}} {\tan (angle)} <math>
Solar parallax
After Johannes Kepler discovered his Third Law, it was possible to build a scale model of the whole solar system, but without the scale. To fix the scale, it suffices to measure one distance within the solar system, e.g., the mean distance from the Earth to the Sun or astronomical unit (AU). When done by triangulation, this is referred to as the solar parallax, the difference in position of the Sun as seen from the Earth's centre and a point one Earth radius away, i.e., the angle subtended at the Sun by the Earth's mean radius. Knowing the solar parallax and the mean Earth radius allows one to calculate the AU, the first, small step on the long road of establishing the size — and thus the minimum age — of the visible Universe.
A primitive way of determining the distance to the Sun in terms of the distance to the Moon was already proposed by Aristarchus: if the Sun is relatively close by, the first and last quarters of the Moon will not happen in time precisely in the middle between new and full moon. Unfortunately the method (which unrealistically assumes regular circular motion for the Moon) becomes progressively imprecise for solar distances much larger than the distance of the Moon, and Aristachus obtained a nonsensical result. It is, however, in essence a parallax method.
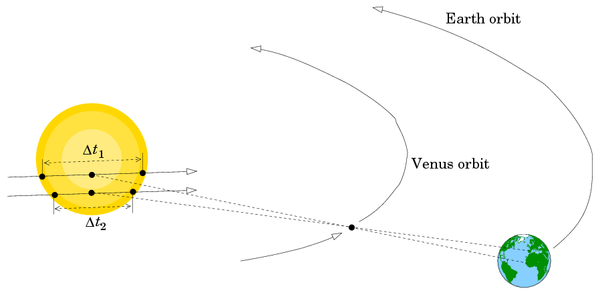
It was proposed by Edmund Halley in 1716, that the transit of Venus over the solar disc be used to derive the solar parallax. And so it was done in 1761 and 1769. There is the famous story of the French astronomer Guillaume Le Gentil, who travelled to India to observe the 1761 event, but didn't reach his destination in time due to war. He stayed on for the 1769 event, but then there were clouds blocking the Sun...
The use of Venus transits was less successful than had been hoped due to the black drop effect.
Much later, the solar system was 'scaled' using the parallax of asteroids, some of which, like Eros, pass much closer to Earth than Venus. In a favourable opposition, Eros can approach the Earth to within 22 million kilometres. Both the opposition of 1901 and that of 1930/1931 were used for this purpose, the calculations of the latter determination being completed by Astronomer Royal Sir Harold Spencer Jones.
Also radar reflections, both off Venus (1958) and off asteroids, like Icarus, have been used for solar parallax determination. Today, use of spacecraft telemetry links has solved this old problem completely.
Stellar parallax
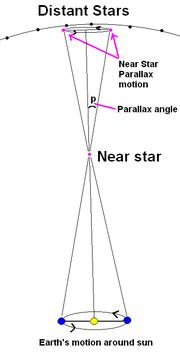
On an interstellar scale, parallax created by the different orbital positions of the Earth causes the stars to seem to move.
The annual parallax is defined as the difference in position of a star as seen from the Earth and Sun, i.e. the angle subtended at a star by the mean radius of the Earth's orbit around the Sun. Given two points on opposite ends of the orbit, the parallax is half the maximum parallactic shift evident from the star viewed from the two points. The parsec is the distance for which the annual parallax is 1 arcsecond. A parsec equals 3.26 light years.
The distance of an object (in parsecs) can be computed as the reciprocal of the parallax. For instance, the nearest star, Alpha Centauri, has a parallax of 0.750". Therefore the distance is 1/0.750=1.33 parsecs or about 4.3 light years.
Computation
The parallax <math>p'' = \frac {au} {d} \cdot 180 \cdot \frac {3600} {\pi} <math> in arc seconds
where
- au = astronomical unit = Average distance from sun to earth = 1.4959 · 1011 m
- d = distance to the star
Picking a good unit of measure will cancel the constants. Derivation:
- right triangle
- <math>\sin p = \frac {au} {d} <math>
- small angle approximation
- <math>\sin x ~= x\textrm{\ radians} = x \cdot \frac {180} {\pi} \textrm{\ degrees} = x \cdot 180 \cdot \frac {3600} {\pi} <math> arcseconds
- parallax <math>p'' ~= \frac {au} {d} \cdot 180 \cdot \frac{3600} {\pi} <math>
- If the parallax is 1", then the distance is <math>d = au \cdot 180 \cdot \frac {3600} {\pi} <math> = 206264 au = 3.2616 lyr = 1 parsec (This defines the parsec)
- The parallax <math>p = \frac {1} {d} <math> arcseconds, when the distance is given in parsecs
The fact that stellar parallax was so small that it was unobservable at the time was used as the main scientific argument against heliocentrism during the early modern age. It is clear from Euclid's geometry that the effect would be undetectable if the stars were far enough away; but for various reasons such a gigantic size seemed entirely implausible.
Measurements of the annual parallax as the earth goes through its orbit was the first reliable way to determine the distances to the closest stars. This method was first used by Friedrich Wilhelm Bessel in 1838 when he measured the distance to 61 Cygni, and it remains the standard for calibrating other measurement methods (after the size of the orbit of the earth is measured by radar reflection on other planets). In 1989, a satellite called "Hipparcos" was launched with the main purpose of obtaining parallaxes and proper motions of nearby stars, increasing the reach of the method ten-fold.
Dynamic or moving-cluster parallax
The open stellar cluster 'Hyades' (Rain Stars) in Taurus extends over such a large part of the sky, 20 degrees, that the proper motions as derived from astrometry appear to converge with some precision to a perspective point north of Orion. Combining the observed apparent (angular) proper motion in seconds of arc with the also observed true (absolute) receding motion as witnessed by the Doppler redshift of the stellar spectral lines, allows us to estimate the distance of the cluster and its member stars in much the same way as using annual parallax.
Dynamic parallax has sometimes also been used to determine the distance to a supernova, when the optical wave front of the outburst was seen to propagate through the surrounding dust clouds at an apparent angular velocity, when we know its true propagation velocity to be that of light.
The scale of the Universe
All these various astronomical parallax methods allow us to establish the first rungs on the cosmic scale ladder, out to a few hundred light years. Beyond that, other methods must be taken into use: e.g., "spectroscopic parallaxes" — not really parallaxes at all. It is a prototype of a "standard candle" method, where we observe the apparent brightness of an object we know, based on some physical theory, the true brightness of. For groups of stars we have the Hertzsprung-Russell diagram which allows us to derive a star's absolute brightness or magnitude <math>M<math> from its spectral type. The observed (apparent) brightness or magnitude being <math>m<math>, we can then derive its parallax <math>p<math> by
- <math>
5 \log p + 5 = M - m \,
<math>
called "spectroscopic parallax".
Further methods, mostly of the "standard candle" variety, are the variable stars called Cepheids — the absolute brightness of which depends on their observed period of variation —, supernova brightnesses, globular cluster sizes and brightnesses, complete galaxy brightnesses etc. These are all much more uncertain as they are not based on simple geometry. Yet, parallaxes are the basis of everything, as they allow the calibration of these more uncertain methods in the Solar neighbourhood.
A very modern method which is not a traditional parallax method but also geometric in nature, is "gravitational lensing parallax". It depends on observing the differential time delay of brightness variations from a remote quasar reaching us by two different paths through the gravitational field or "lens" of a foreground galaxy. If the redshifts of both the quasar and the foreground galaxy are known, one can show that the absolute distances of both are proportional to the differential delay, and can in fact be calculated given also the geometry of the gravitational lens on the celestial sphere.
All these independent techniques aim at determining Hubble's constant, the constant describing how the redshift of galaxies, due to the Universe's expansion, depends on these galaxies' distance from us. Knowing Hubble's constant again allows us to determine, by simply running the film of the cosmic expansion backwards, how long ago it was when all these galaxies were collected in a single point -- the Big Bang. Current knowledge puts this at some 14.7 billion years ago, but with considerable uncertainty and dependence on various model assumptions.
Parallax as a metaphor
In a philosophic/geometric sense: An apparent change in the direction of an object, caused by a change in observational position that provides a new line of sight. The apparent displacement, or difference of position, of an object, as seen from two different stations, or points of view.
External links
- Java applet demonstrating stellar parallax (http://instruct1.cit.cornell.edu/courses/astro101/java/parallax/parallax.html)
- BBC's Sky at Night (http://www.bbc.co.uk/science/space/realmedia/skymedia_justnotcricket.ram) programme: Patrick Moore demonstrates Parallax using Cricket. (Requires RealPlayer)bg:Паралакс
ca:Paral·laxi de:Parallaxe es:Paralaje et:Parallaks fr:parallaxe he:היסט io:Paralaxo it:Parallasse nl:parallax pl:paralaksa ru:Параллакс
Categories: Optics | Computer vision | Vision | Angle