Kepler's laws of planetary motion
|
|
Johannes Kepler's primary contributions to astronomy/astrophysics were his three laws of planetary motion. Kepler, a nearly blind though brilliant German mathematician, derived these laws, in part, by studying the observations of the keen-sighted Danish astronomer Tycho Brahe. Sir Isaac Newton would later design his laws of motion and universal gravitation and verify that Kepler's laws could be derived from them.
| Contents |
Kepler's laws of planetary motion
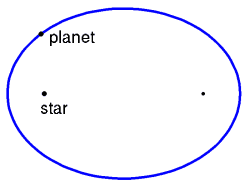
- Kepler's first law (1609): The orbit of a planet about a star is an ellipse with the star at one focus.
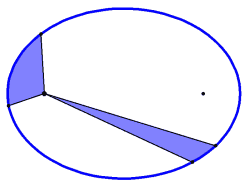
- Kepler's second law (1609): A line joining a planet and its star sweeps out equal areas during equal intervals of time.
- Kepler's third law (1618): The square of the sidereal period of an orbiting planet is directly proportional to the cube of the orbit's semimajor axis.
Kepler's first law
The orbit of a planet about a star is an ellipse with the star at one focus.
There is no object at the other focus of a planet's orbit. The semimajor axis, a, is half the major axis of the ellipse. In some sense it can be regarded as the average distance between the planet and its star, but it is not the time average in a strict sense, as more time is spent near apocentre than near pericentre.
Connection with Newton's laws
Newton proposed that "every object in the universe attracts every other object along a line of the centers of the objects proportional to each objects mass, and inversely proportional to the square of the distance between the objects."
This section proves that Kepler's first law is consistent with Newton's laws of motion. We begin with Newton's law F=ma:
- <math>m\frac{d^2\mathbf{r}}{dt^2} = f(r)\widehat{\mathbf{r}}<math>
Here we express F as the product of its magnitude and its direction. Recall that in polar coordinates:
- <math>\frac{d\mathbf{r}}{dt} = \dot r\widehat{\mathbf{r}} + r\dot\theta\widehat{\theta}<math>
- <math>\frac{d^2\mathbf{r}}{dt^2} = (\ddot r - r\dot\theta^2)\widehat{\mathbf{r}} + (r\ddot\theta + 2\dot r \dot\theta)\widehat{\theta}<math>
In component form we have:
- <math>m(\ddot r - r\dot\theta^2) = f(r)<math>
- <math>m(r\ddot\theta + 2\dot r\dot\theta) = 0<math>
Now consider the angular momentum:
- <math>\mathbf{L} = \left|\mathbf{r} \times m\frac{d\mathbf{r}}{dt}\right| = \left|mr^2\dot\theta\right|<math>
So:
- <math>r^2\dot\theta = \ell<math>
where <math>\ell=L/m<math> is the angular momentum per unit mass. Now we substitute. Let:
- <math>r = \frac{1}{u}<math>
- <math>\dot r = -\frac{1}{u^2}\dot u = -\frac{1}{u^2}\frac{d\theta}{dt}\frac{du}{d\theta}= -\ell\frac{du}{d\theta}<math>
- <math>\ddot r = -\ell\frac{d}{dt}\frac{du}{d\theta} = -\ell\dot\theta\frac{d^2u}{d\theta^2}= -\ell^2u^2\frac{d^2u}{d\theta^2}<math>
The equation of motion in the <math>\hat{\mathbf{r}}<math> direction becomes:
- <math>\frac{d^2u}{d\theta^2} + u = - \frac{1}{m\ell^2u^2}f\left(\frac{1}{u}\right)<math>
Newton's law of gravitation states that the central force is inversely proportional to the square of the distance so we have:
- <math>\frac{d^2u}{d\theta^2} + u = \frac{k}{m\ell^2}<math>
where k is our proportionality constant.
This differential equation has the general solution:
- <math>u = A\cos(\theta-\theta_0) + \frac{k}{m\ell^2}.<math>
Replacing u with r and letting θ0=0:
- <math>r = \frac{1}{A\cos\theta + \frac{k}{m\ell^2}}<math>.
This is indeed the equation of a conic section with the origin at one focus. Q.E.D.
Kepler's second law
A line joining a planet and its star sweeps out equal areas during equal intervals of time.
This is also known as the law of equal areas. Suppose a planet takes 1 day to travel from points A to B. During this time, an imaginary line, from the Sun to the planet, will sweep out a roughly triangular area. This same amount of area will be swept every day.
As a planet travels in its elliptical orbit, its distance from the Sun will vary. As an equal area is swept during any period of time and since the distance from a planet to its orbiting star varies, one can conclude that in order for the area being swept to remain constant, a planet must vary in velocity. Planets move fastest when at perihelion and slowest when at aphelion.
This law was developed, in part, from the observations of Brahe that indicated that the velocity of planets was not constant.
This law corresponds to the angular momentum conservation law in the given situation.
Proof of Kepler's second law:
Assuming Newton's laws of motion, we can show that Kepler's second law is consistent. By definition, the angular momentum <math>\mathbf{L}<math> of a point mass with mass <math>m<math> and velocity <math>\mathbf{v}<math> is :
- <math>\mathbf{L} \equiv m \mathbf{r} \times \mathbf{v}<math>.
where <math>\mathbf{r}<math> is the position vector of the particle.
Since <math>\mathbf{v} = \frac{d\mathbf{r}}{dt} <math>, we have:
- <math>\mathbf{L} = \mathbf{r} \times m\frac{d\mathbf{r}}{dt}<math>
taking the time derivative of both sides:
- <math>\frac{d\mathbf{L}}{dt} = \mathbf{r} \times \mathbf{F} = 0 <math>
since the cross product of parallel vectors is 0. We can now say that <math>|\mathbf{L}|<math> is constant.
The area swept out by the line joining the planet and the sun, is half the area of the parallelogram formed by <math>\mathbf{r}<math> and <math>d\mathbf{r}<math>.
- <math>dA = \begin{matrix}\frac{1}{2}\end{matrix} |\mathbf{r} \times d\mathbf{r}| = \begin{matrix}\frac{1}{2}\end{matrix} \left|\mathbf{r} \times \frac{d\mathbf{r}}{dt}dt\right| = \frac{\mathbf{|L|}}{2m}dt<math>
Since <math>|\mathbf{L}|<math> is constant, the area swept out by is also constant. Q.E.D.
Kepler's third law (harmonic law)
The square of the sidereal period of an orbiting planet is directly proportional to the cube of the orbit's semimajor axis.
- P2 ~ a3
- P = object's sidereal period in years
- a = object's semimajor axis, in AU
Thus, not only does the length of the orbit increase with distance, also the orbital speed decreases, so that the increase of the sidereal period is more than proportional.
See the actual figures: attributes of major planets.
Newton would modify this third law, noting that the period is also affected by the orbiting body's mass, however typically the central body is so much more massive that the orbiting body's mass may be ignored. (See below.)
Applicability
The laws are applicable whenever a comparatively light object revolves around a much heavier one because of gravitational attraction. It is assumed that the gravitational effect of the lighter object on the heavier one is negligible. An example is the case of a satellite revolving around Earth. By using the reduced mass and the relative separation of two bodies of any relative mass (even equal) the two-body problem can be reduced to an equivalent one-body problem (as if there were one very large mass and one orbiter of negligible mass). Then Kepler's laws apply to that system without the restriction of one body's being "light". In that case, however, the Third Law applies only to the two given bodies. In other words, if the same pair of bodies is initiated in orbit with different semi-major axes, then the periods of these intercompared cases will follow Kepler's Third Law, but additional bodies must not be introduced.
Application
Assume an orbit with semimajor axis a, semiminor axis b, and eccentricity ε. To convert the laws into predictions, Kepler began by adding the orbit's auxiliary circle (that with the major axis as a diameter) and defined these points:
- c center of auxiliary circle and ellipse
- s sun (at one focus of ellipse); <math>\mbox{length }cs=a\varepsilon<math>
- p the planet
- z perihelion
- x is the projection of the planet to the auxiliary circle; then <math>\mbox{area }sxz=\frac ba\mbox{area }spz<math>
- y is a point on the circle such that <math>\mbox{area }cyz=\mbox{area }sxz=\frac ba\mbox{area }spz<math>
and three angles measured from perihelion:
- true anomaly <math>T=\angle zsp<math>, the planet as seen from the sun
- eccentric anomaly <math>E=\angle zcx<math>, x as seen from the centre
- mean anomaly <math>M=\angle zcy<math>, y as seen from the centre
Missing image
Kepler's-equation-scheme.png
image:kepler's-equation-scheme.png
Then
- <math>\mbox{area }cxz=\mbox{area }cxs+\mbox{area }sxz<math><math>=\mbox{area }cxs+\mbox{area }cyz<math>
- <math>\frac{a^2}2E=a\varepsilon\frac a2\sin E+\frac{a^2}2M<math>
giving Kepler's equation
- <math>M=E-\varepsilon\sin E<math>.
To connect E and T, assume <math>r=\mbox{length }sp<math> then
- <math>a\varepsilon+r\cos T=a\cos E<math> and <math>r\sin T=b\sin E<math>
- <math>r=\frac{a\cos E-a\varepsilon}{\cos T}=\frac{b\sin E}{\sin T}<math>
- <math>\tan T=\frac{\sin T}{\cos T}=\frac ba\frac{\sin E}{\cos E-\varepsilon}=\frac{\sqrt{1-\varepsilon^2}\sin E}{\cos E-\varepsilon}<math>
which is ambiguous but useable. A better form follows by some trickery with trigonometric identities:
- <math>\tan\frac T2=\sqrt\frac{1+\varepsilon}{1-\varepsilon}\tan\frac E2<math>
(So far only laws of geometry have been used.)
Note that <math>\mbox{area }spz<math> is the area swept since perihelion; by the second law, that is proportional to time since perihelion. But we defined <math>\mbox{area }spz=\frac ab\mbox{area }cyz=\frac ab\frac{a^2}2M<math> and so M is also proportional to time since perihelion—this is why it was introduced.
We now have a connection between time and position in the orbit. The catch is that Kepler's equation cannot be rearranged to isolate E; going in the time-to-position direction requires an iteration (such as Newton's method) or an approximate expression, such as
- <math>E\approx M+\left(\varepsilon-\frac18\varepsilon^3\right)\sin M+\frac12\varepsilon^2\sin 2M+\frac38\varepsilon^3\sin 3M<math>
via the Lagrange reversion theorem. For the small ε typical of the planets (except Pluto) such series are quite accurate with only a few terms; one could even develop a series computing T directly from M.[1] (http://info.ifpan.edu.pl/firststep/aw-works/fsII/mul/mueller.html)
Kepler's understanding of the laws
Kepler did not understand why his laws were correct; it was Isaac Newton who discovered the answer to this more than fifty years later. Newton, understanding that his third law of motion was related to Kepler's third law of planetary motion, devised the following:
- <math>P^2 = \frac{4\pi^2}{G(m_1 + m_2)} \cdot a^3<math>
where:
- P = object's sidereal period
- a = object's semimajor axis
- G = 6.67 × 10−11 N · m2/kg2 = the gravitational constant
- m1 = mass of object 1
- m2 = mass of object 2
- π = mathematical constant pi
Astronomers doing celestial mechanics often use units of years, AU, G=1, and solar masses, and with m2<<m1, this reduces to Kepler's form. SI units may also be used directly in this formula.
See also
de:Keplersche Gesetze es:Leyes de Kepler fr:Lois de Kepler it:Leggi di Keplero he:חוקי קפלר hu:Kepler-törvények nl:Wetten van Kepler ja:ケプラーの法則 pl:Prawa Keplera sl:Keplerjevi zakoni zh:开普勒定律