|
|
- Möbius transformations should not be confused with the Möbius transform.
In mathematics, a Möbius transformation, also called a homographic function, is a conformal mapping that is a bijection on the extended complex plane (that is, the complex plane augmented by the point at infinity, written ∞.) It is named in honor of August Ferdinand Möbius.
Möbius transformations are closely related to the group of isometries of the hyperbolic plane and the hyperbolic 3-manifold. Both the Fuchsian groups and the Kleinian groups are certain discrete subgroups of the group of Möbius transformations; these play an important role in the theory of Riemann surfaces and hyperbolic 3-manifolds. A particularly important subgroup is the modular group; it is central to the theory of many fractals, modular forms, elliptic curves and Pellian equations.
| Contents |
Geometry
With two exceptions given below, the general formula for a Möbius transformation is given by
- <math>w = \frac{a z + b}{c z + d}<math>
where a, b, c, d are any complex numbers satisfying ad - bc ≠ 0. Since multiplying the numerator and the denominator by the same constant gives the same transformation, one usually works with a representative transformation satisfying ad-bc=1. There are two special cases not covered by the formula above:
- the point <math>z = -d/c\,<math> is mapped to <math>w=\infty<math>
- the point <math>z=\infty<math> is mapped to <math>w = a/c\,<math>
We can have Möbius transformations over the real numbers, as well as for the complex numbers. In both cases, we need to augment the domain with a point at infinity.
It can be shown that the inverse and composition of two Möbius transformations are similarly defined, and so the Möbius transformations form a group under composition - called the Möbius group.
The geometric interpretation of the Möbius group is that it is the group of automorphisms of the Riemann sphere. The bilinear transform is a special case of a Möbius transformation.
Any Möbius map can be composed from the elementary transformations - dilations, translations and inversions. If we define a line to be a circle passing through infinity, then it can be shown that a Möbius transformation maps circles to circles, by looking at each elementary transformation.
The Möbius transformation cross-ratio preservation theorem states that the cross-ratio
- <math>
\frac{(w_1-w_2)(w_3-w_4)}{(w_1-w_4)(w_3-w_2)} = \frac{(z_1-z_2)(z_3-z_4)}{(z_1-z_4)(z_3-z_2)} <math> is invariant under a Möbius transformation that maps from z to w.
Equations
The transformation
- <math>w = \frac{a z + b}{c z + d}<math>
can be usefully expressed as a matrix
- <math>\mathfrak{H} = \begin{pmatrix} a & b \\ c & d \end{pmatrix}<math>
In this form, the matrix may be multiplied by any scalar λ and still represent the same transformation. This means that a Möbius transformation on C therefore has six real degrees of freedom.The matrix view of a Möbius transformation corresponds to a projectivity on the projective line over C.
Composition
Let <math>\mathfrak{H}_1, \mathfrak{H}_2<math> be two Möbius transformations:
- <math>
\mathfrak{H}_1 = \begin{pmatrix} a_1 & b_1 \\ c_1 & d_1 \end{pmatrix}, \;\;
\mathfrak{H}_2 = \begin{pmatrix} a_2 & b_2 \\ c_2 & d_2 \end{pmatrix}<math>
If these transformations are carried out in succession, first <math>z_1 = \mathfrak{H}_1(z)<math> then <math>Z = \mathfrak{H}_2(z_1)<math> to obtain <math>Z = \mathfrak{H}_2[\mathfrak{H}_1(z)]<math>, the result can be readily seen to be another Möbius transformation <math>\mathfrak{H}_3<math> which appears as the product of the two matrices <math>\mathfrak{H}_1, \mathfrak{H}_2<math>
- <math>\mathfrak{H}_3 = \mathfrak{H}_2 \mathfrak{H}_1 =
\begin{pmatrix} a_2 a_1 + b_2 c_1 & a_2 b_1 + b_2 d_1 \\ c_2 a_1 + d_2 c_1 & c_2 b_1 + d_2 d_1 \end{pmatrix} <math>
Thus, Möbius transformations form a group.
Inversion
The inverse of a Möbius transformation <math>\mathfrak{H}<math> can be derived as
- <math>z = \mathfrak{H}^{-1}(Z) = \frac{d Z - b}{-c Z + a}<math>
and so
- <math>\mathfrak{H}^{-1} = \begin{pmatrix} \;\;d & -b \\ -c & \;\;a \end{pmatrix}<math>
Classification
Möbius transformations are commonly classified into four types, parabolic, elliptic, hyperbolic and loxodromic. The classification has both algebraic and geometric significance. Geometrically, the different types result in different transformations of the complex plane, as the figures below illustrate. These types can be distinguished by looking at the trace <math>\mbox{tr}\,\mathfrak{H}=a+d<math>. Note that the trace is invariant under conjugation, that is,
- <math>\mbox{tr}\,\mathfrak{GHG}^{-1} = \mbox{tr}\,\mathfrak{H}<math>
and so every member of a conjugacy class will have the same trace. Every Möbius transformation can be written such that its representing matrix <math>\mathfrak{H}<math> has determinant one (by multiplying the entries with a suitable scalar). Two Möbius transformations <math> \mathfrak{H}, \mathfrak{H}'<math> (both not equal to the identity transform) with <math> \det \mathfrak{H}=\det\mathfrak{H}'=1 <math> are conjugate if and only if <math> \mbox{tr}^2\,\mathfrak{H}= \mbox{tr}^2\,\mathfrak{H}' <math>.
In the following discussion we will always assume that the representing matrix <math> \mathfrak{H}<math> is normalized such that <math> \det{\mathfrak{H}}=ad-bc=1 <math>.
Parabolic transforms The transform is said to be parabolic if
- <math>\mbox{tr}^2\mathfrak{H} = (a+d)^2 = 4<math>.
A transform is parabolic if and only if it has one fixed point in the compactified complex plane <math>\hat{\mathbb{C}}=\mathbb{C}\cup\{\infty\}<math>. It is parabolic if and only if it is conjugate to
- <math>\begin{pmatrix} 1 & 1 \\ 0 & 1 \end{pmatrix}<math>.
All other non-identity transformations have two fixed points. All non-parabolic (non-identity) transforms are conjugate to
- <math>\begin{pmatrix} \lambda & 0 \\ 0 & \lambda^{-1} \end{pmatrix}<math>
with <math>\lambda<math> not equal to 0,1 or -1. The square <math>k=\lambda^2<math> is called the characteristic constant or multiplier of the transformation.
Elliptic transforms The transform is said to be elliptic if
- <math>0 \le \mbox{tr}^2\mathfrak{H} < 4<math>.
A transform is elliptic if and only if <math>|\lambda|=1<math>. Writing <math>\lambda=e^{i\alpha}<math>, an elliptic transform is conjugate to
- <math>\begin{pmatrix} \cos\alpha & \sin\alpha \\
-\sin\alpha & \cos\alpha \end{pmatrix}<math>
with <math>\alpha<math> real. Note that for any <math>\mathfrak{H}<math>, the characteristic constant of <math>\mathfrak{H}^n<math> is <math>k^n<math>. Thus, the only Möbius transformations of finite order are the elliptic transformations, and these only when λ is a root of unity; equivalently, when α is a rational number.
Hyperbolic transforms The transform is said to be hyperbolic if
- <math>\mbox{tr}^2\mathfrak{H} > 4<math>.
A transform is hyperbolic if and only if λ is real.
Loxodromic transforms The transform is said to be loxodromic if <math>\mbox{tr}^2\mathfrak{H}<math> is not in the closed interval of [0,4]. Hyperbolic transforms are thus a special case of loxodromic transformations. A transformation is loxodromic if and only if <math>|\lambda|\ne 1<math>. Historically, navigation by loxodrome or rhumb line refers to a path of constant bearing; the resulting path is a logarithmic spiral, similar in shape to the transformations of the complex plane that a loxodromic Möbius transformation makes. See the geometric figures below.
Fixed points
Any Möbius transformation <math>\mathfrak{H}<math> which is not the identity mapping will have two fixed points <math>\gamma_1, \gamma_2<math>, invariant under transformation by <math>\mathfrak{H}<math>. Note that the fixed points are counted here "with multiplicity"; for parabolic transformations, the fixed points coincide. Either or both of these fixed points may be the point at infinity: this will happen when <math>c = 0<math>. If this is the case, then the transformation will be an affine transformation (some combination of rotation, dilation, and translation). If both fixed points are at infinity, then the transformation is a pure translation with parameters <math>a = 1<math>, <math>b=\Delta<math>, <math>c = 0<math>, <math>d=1<math> i.e. the map <math> \gamma \mapsto \gamma+\Delta <math>.
Determination of fixed points
The fixed points are obtained by solving the fixed point equation
- <math> \gamma={{a\gamma +b}\over {c\gamma +d}} <math>.
For <math>c\ne 0<math>, this has two roots
- <math>\gamma =
\frac{(a - d) \pm \sqrt{\mbox{tr}^2\mathfrak{H} - 4\,}}{2c}
<math> (proof)
and, for <math>c=0<math>, one of the fixed points is at
- <math>\gamma=\frac{-b}{a-a^{-1}}<math>
and the other fixed point is the point at infinity. If <math>a=1<math>, then both fixed points are at infinity, and the Möbius transform corresponds to a pure translation. The above formulas presume the normalization ad-bc=1.
Construction of Möbius transformations with prescribed fixed points
Non-parabolic case:
Let us first discuss the case where the transformation has two different fixed points which are finite.
A Möbius <math>\mathfrak{H}<math> transformation is uniquely defined by its set of fixed points <math>\{\gamma_1, \gamma_2 \}<math> together with the characteristic constant <math>k<math>:
- <math>\mathfrak{H}(k;\gamma_1,\gamma_2) =
\begin{pmatrix}
k \gamma_2 - \gamma_1 & (1 - k) \gamma_1 \gamma_2 \\ k - 1 & \gamma_2 - k \gamma_1
\end{pmatrix} <math> The representation is unique once the two fixed points have been suitably labeled; the two matrices <math> \mathfrak{H}(k;\gamma_1,\gamma_2)<math> and <math>\mathfrak{H}({1\over k};\gamma_2,\gamma_1) <math> define the same Möbius transformation. The above transform can be written in a normalized form by multiplying each entry with the (non-zero) scalar <math> c={{1}\over{\gamma_2-\gamma_1}}<math>. The resulting matrix <math>{\mathfrak{H}}' <math> representing the same Möbius transformation has matrix trace equal to k+1 and determinant equal to k. This implies that the characteristic polynomial of the matrix <math>{\mathfrak{H}}' <math> has roots <math> \lambda_1, \, \lambda_2 <math> equal to <math>\,\lambda_1=k <math>, <math>\, \lambda_2=1 <math>. Thus the characteristic constant k coincides with one of the two different ratios of eigenvalues <math> \lambda_2 \over \lambda_1 <math> of the matrix representing the transformation (note that each ratio is invariant under multiplication of matrices with non-zero scalars).
Note that every non-parabolic transformation (every transformation having two different fixed points) is conjugate or similar to a linear transformation having one fixed point at infinity and another at 0, i.e the map <math>z \mapsto kz<math> given by
- <math>\begin{pmatrix} \lambda & 0 \\ 0 & \lambda^{-1} \end{pmatrix}<math>
with <math>k=\lambda^2<math>.
Parabolic case:
If there is only one (finite) fixed point <math> \gamma <math> then the Möbius transformation is of the form
- <math>\mathfrak{H} =
\begin{pmatrix}
1+\gamma\beta & - \beta \gamma^2 \\ \beta & 1-\gamma \beta
\end{pmatrix} <math> where β is called the translation length.
Normal form
The fixed point expressions are also sometimes written in the so-called normal form. For the non-parabolic case, this form is
- <math>\frac {w(z)-\gamma_1}{w(z)-\gamma_2} =
k \frac {z-\gamma_1}{z-\gamma_2} <math>
where
- <math>w(z)=\frac {az+b}{cz+d}<math>.
It is for this reason that the characteristic constant is sometimes called the multiplier. Note that for the derivatives, one has
- <math>w'(\gamma_1)= k<math>
and
- <math>w'(\gamma_2)= 1/k<math>
Thus, once the multiplier is fixed, the two fixed points can be distinguished. In general, whenever <math>|k|>1<math>, one says that <math>\gamma_1<math> is the repulsive fixed point, and <math>\gamma_2<math> is the attractive fixed point. For <math>|k|<1<math>, the roles are reversed.
In the parabolic case, the normal form can be written as
- <math>\frac{1}{w(z)-\gamma} = \frac{1}{z-\gamma} + \beta<math>.
Here, β is called the translation length. When the fixed point γ is at infinity, one then has <math>-\gamma^2\beta<math> being finite and non-zero, corresponding to the translation <math>z\to z-\gamma^2\beta<math>.
Geometric interpretation of the characteristic constant
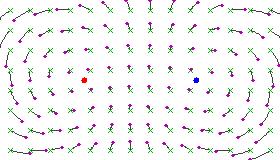
The following picture depicts the two fixed points of a Möbius transformation in the non-parabolic case:
The characteristic constant can be expressed in terms of its logarithm:
- <math>e^{\rho + \alpha i} = k \;<math>
When expressed in this way, <math>\rho<math> becomes an expansion factor. It indicates how repulsive the fixed point <math>\gamma_1<math> is, and how attractive <math>\gamma_2<math> is. If <math>\rho = 0<math>, then the fixed points are neither attractive nor repulsive but indifferent, and the transformation is said to be elliptical. These transformations tend to move all points in circles around the two fixed points . If one of the fixed points is at infinity, the this is equivalent to doing an affine rotation around a point.
Missing image
Mobius_Small_Neg_Elliptical.jpeg
Image:Mobius_Small_Neg_Elliptical.jpeg
Missing image
Mobius_Large_Neg_Elliptical.jpeg
Image:Mobius_Large_Neg_Elliptical.jpeg
 Missing image
Missing image
Mobius_Large_Pos_Elliptical.jpeg
Image:Mobius_Large_Pos_Elliptical.jpeg
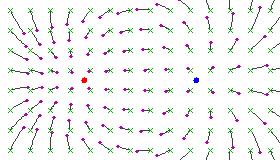
<math>\alpha<math> is a rotation factor, indicating to what extent the transform rotates the plane anti-clockwise about <math>\gamma_1<math> and clockwise about <math>\gamma_2<math>. If <math>\alpha<math> is zero (or a multiple of <math>2 \pi<math>), then the transformation is said to be hyperbolic. These transformations tend to move points along circular paths from one fixed point toward the other.
 Missing image
Missing image
Mobius_Large_Neg_Hyperbolic.jpeg
Image:Mobius_Large_Neg_Hyperbolic.jpeg
Missing image
Mobius_Small_Pos_Hyperbolic.jpeg
Image:Mobius_Small_Pos_Hyperbolic.jpeg
Missing image
Mobius_Large_Pos_Hyperbolic.jpeg
Image:Mobius_Large_Pos_Hyperbolic.jpeg
- I'ts not surprising that these look very much like the field lines of bar magnets. Circular arcs are those that subtend a constant angle between two points.
If both ρ and α are nonzero, then the transformation is said to be loxodromic. These transformations tend to move all points in S-shaped paths from one fixed point to the other.
Missing image
Mobius_Small_Loxodromic.jpeg
Image:Mobius_Small_Loxodromic.jpeg
Missing image
Mobius_Large_Loxodromic.jpeg
Image:Mobius_Large_Loxodromic.jpeg
Iterating a transformation
If a transformation <math>\mathfrak{H}<math> has fixed points <math>\gamma_1, \gamma_2<math>, and expansion and rotation factors <math>\rho<math> and <math>\alpha<math>, then <math>\mathfrak{H}' = \mathfrak{H}^n<math> will have <math>\gamma_1' = \gamma_1, \gamma_2' = \gamma_2, \rho' = n\rho, \alpha' = n\alpha<math>.
This can be used to continuously iterate a transformation.
These images show three points (red, blue and black) continuously iterated under transformations with various characteristic constants
Missing image
Mobius23621.jpeg
Image:Mobius23621.jpeg
Missing image
Mobius23622.jpeg
Image:Mobius23622.jpeg
 Missing image
Missing image
Mobius23624.jpeg
Image:Mobius23624.jpeg
Missing image
Mobius23625.jpeg
Image:Mobius23625.jpeg
Poles of the transformation
The point
- <math>z_\infty = - \frac{d}{c}<math>
is called the pole of <math>\mathfrak{H}<math>; it is that point which is transformed to the point at infinity under <math>\mathfrak{H}<math>.
The inverse pole
- <math>Z_\infty = \frac{a}{c}<math>
Is that point to which the point at infinity is transformed. The point midway between the two poles is always the same as the point midway between the two fixed points:
- <math>\gamma_1 + \gamma_2 = z_\infty + Z_\infty<math>
These four points are the vertices of a parallelogram which is sometimes called the characteristic parallelogram of the transformation.
A transform <math>\mathfrak{H}<math> can be specified with two fixed points <math>\gamma_1, \gamma_2<math> and the pole <math>z_\infty<math>.
- <math>\mathfrak{H} =
\begin{pmatrix}
Z_\infty & - \gamma_1 \gamma_2 \\ 1 & - z_\infty
\end{pmatrix}, \;\;
Z_\infty = \gamma_1 + \gamma_2 - z_\infty
<math>
This allows us to derive a formula for conversion between <math>k<math> and <math>z_\infty<math> given <math>\gamma_1, \gamma_2<math>:
- <math>z_\infty = \frac{k \gamma_1 - \gamma_2}{1 - k}<math>
- <math>k
= \frac{\gamma_2 - z_\infty}{\gamma_1 - z_\infty} = \frac{Z_\infty - \gamma_1}{Z_\infty - \gamma_2} = \frac {a - c \gamma_1}{a - c \gamma_2}<math>
Which reduces down to
- <math>k = \frac{(a + d) + \sqrt {(a - d)^2 + 4 b c}}{(a + d) - \sqrt {(a - d)^2 + 4 b c}}<math>
The last expression coincides with one of the (mutually reciprocal) eigenvalue ratios <math> \lambda_1\over \lambda_2<math> of the matrix
- <math>\mathfrak{H} =
\begin{pmatrix}
a & b \\ c & d
\end{pmatrix} <math> representing the transform (compare the discussion in the preceding section about the characteristic constant of a transformation). Its characteristic polynomial is equal to
- <math>
\mbox{det} (\lambda I_2- \mathfrak{H})
=\lambda^2-\mbox{tr} \mathfrak{H}\,\lambda+ \mbox{det} \mathfrak{H} =\lambda^2-(a+d)\lambda+(ad-bc) <math> which has roots
- <math> \lambda_{i}=\frac{(a + d) \pm \sqrt {(a - d)^2 + 4 b c}}{2}=\frac{(a + d) \pm \sqrt {(a + d)^2 - 4(ad-b c)}}{2} \ .
<math>
Specifying a transformation by three points
Direct approach
Any set of three points
- <math>
Z_1 = \mathfrak{H}(z_1), \;\;
Z_2 = \mathfrak{H}(z_2), \;\;
Z_3 = \mathfrak{H}(z_3)<math>
uniquely defines a transformation <math>\mathfrak{H}<math>. To calculate this out, it is handy to make use of a transformation that is able to map three points onto (0,0), (1, 0) and the point at infinity.
- <math>\mathfrak{H}_1 = \begin{pmatrix}
\frac{z_2 - z_3}{z_2 - z_1} & -z_1 \frac{z_2 - z_3}{z_2 - z_1} \\ 1 & -z_3 \end{pmatrix}, \;\; \mathfrak{H}_2 = \begin{pmatrix} \frac{Z_2 - Z_3}{Z_2 - Z_1} & -Z_1 \frac{Z_2 - Z_3}{Z_2 - Z_1} \\ 1 & -Z_3 \end{pmatrix} <math>
One can get rid of the infinities by multiplying out by <math>z_2 - z_1<math> and <math>Z_2 - Z_1<math> as previously noted.
- <math>\mathfrak{H}_1 = \begin{pmatrix}
z_2 - z_3 & z_1 z_3 - z_1 z_2 \\ z_2 - z_1 & z_1 z_3 - z_3 z_2 \end{pmatrix} , \;\; \mathfrak{H}_2 = \begin{pmatrix} Z_2 - Z_3 & Z_1 Z_3 - Z_1 Z_2 \\ Z_2 - Z_1 & Z_1 Z_3 - Z_3 Z_2 \end{pmatrix} <math>
The matrix <math>\mathfrak{H}<math> to map <math>z_{1,2,3}<math> onto <math>Z_{1,2,3}<math> then becomes
- <math>\mathfrak{H} = \mathfrak{H}_2^{-1} \mathfrak{H}_1<math>
You can multiply this out, if you want, but if you are writing code then it's easier to use temporary variables for the middle terms.
Alternate method using cross-ratios of point quadruples
This construction exploits the fact (mentioned in the first section) that the cross-ratio
- <math>
\mbox{cr}(z_1,z_2,z_3,z_4)= {{(z_1-z_3)(z_2-z_4)}\over{(z_1-z_4)(z_2-z_3)}} <math> is invariant under a Möbius transformation mapping a quadruple <math> (z_1,z_2,z_3,z_4) <math> to <math> (w_1,w_2,w_3,w_4) <math> via <math>w_i=\mathfrak{H}z_i<math>. If <math>\mathfrak{H}<math> maps a triple <math> (z_1,z_2,z_3) <math> of pairwise different zi to another triple <math> (w_1,w_2,w_3) <math>, then the Möbius transformation <math>\mathfrak{H}<math> is determined by the equation
- <math>
\mbox{cr}(\mathfrak{H}(z),w_1,w_2,w_3)=\mbox{cr}(z,z_1,z_2,z_3) <math> or written out in concrete terms:
- <math>
{{(\mathfrak{H}(z)-w_2)(w_1-w_3)} \over{(\mathfrak{H}(z)-w_3)(w_1-w_2)}} ={{(z-z_2)(z_1-z_3)}\over{(z-z_3)(z_1-z_2)}}\ . <math>
The last equation can be transformed into
- <math>
{{\mathfrak{H}(z)-w_2} \over{\mathfrak{H}(z)-w_3}} ={{(z-z_2)(w_1-w_2)(z_1-z_3)}\over{(z-z_3)(w_1-w_3)(z_1-z_2)}} \ . <math> Solving this equation for <math> \mathfrak{H}(z) <math> one obtains the sought transformation.
References
Not to be confused with:
See also
- Fuchsian group
- Hyperbolic geometry
- Inversive ring geometry
- Kleinian group
- Modular group
- Poincaré half-plane model
- Projective geometry
References
- Svetlana Katok, Fuchsian Groups (1992), University of Chicago Press, Chicago ISBN 0-226-42583-5 (See chapter 2).
- Alan F. Beardon, The Geometry of Discrete Groups (1995), Graduate Texts in Mathematics, vol. 91, Springer Verlag, New York, ISBN 0-3879-0788-2.
- Hershel M. Farkas, Irwin Kra, Theta Constants, Riemann Surfaces and the Modular Group, American Mathematical Society, Providence RI, ISBN 0-8218-1392-7 (See chapter 1. This is a very advanced reference, and only covers Möbius transformations in a very condensed form in the first four pages.)
External link
A java applet allowing you to specify a transformation via its fixed points and so on may be found here (http://www.users.bigpond.com/pmurray/Java/MoebApplet.html).
This page contains material from this article (http://planetmath.org/encyclopedia/MobiusTransformation.html) and this article (http://planetmath.org/?method=src&from=objects&id=4222&op=getobj) at PlanetMath, used under the GFDL by permission.de:Möbiustransformation fr:Transformée de Möbius ru:Дробно-линейное преобразование