Equation of time

During the course of the year, the time as read from a sundial can run ahead of clock time by as much as 16 min 33 s (around October 31–November 1) or fall behind by as much as 14 min 6 s (around February 11–12). This difference, known as the equation of time, results from a combination of the tilt of the Earth's rotation axis and the eccentricity of its orbit. The equation of time is visually illustrated by an analemma.

Naturally, other planets will have an equation of time too. On Mars the difference between sundial time and clock time can be as much as 50 minutes, due to its orbit's considerably greater eccentricity.

Contents

1 Apparent time versus mean time

2 The inclination of the ecliptic

3 The eccentricity of the Earth's orbit

4 More details

5 External links

Apparent time versus mean time

The rotation of the Earth makes a good clock for most purposes because it is very nearly constant, the length of the day increasing only by one second every 45,000 years. For everyday time measurements, it is sufficient to find a convenient way to determine which way the Earth is pointing. Stars would be good, but they are too dim (and too many) at night and are invisible during the day. A useful aid is the Sun, which is out and about when we are and hard to overlook, weather permitting. Unfortunately, the apparent position of the Sun is determined not just by the rotation of the Earth about its axis, but also by the revolution of the Earth around the Sun. The following will explain exactly how this complication arises, and what you can do about it.

The diameter of the Sun as seen from the Earth is about 1/2 degree, so it moves by its own radius every minute.

<math>

\frac{24\ {\rm h}}{360^\circ} \times \frac{60\ {\rm min}}{1\ {\rm h}} \times \left(\frac{1}{4}\right)^\circ = 1\ {\rm min} <math>

That means it will be hard to read a sundial to better than the nearest minute, but then, we don't bother to set our clocks much more accurately than that either. Unfortunately, if we define the second to be constant (say, the fraction 1/31 556 925.974 7 of the tropical year for 1900 January 0 at 12 hours —the "ephemeris second" definition used between 1960 and 1967), then we find that some days (from high noon to high noon) have more than 86,400 seconds, and some have less. The solar Christmas day, for example, was 86,428 seconds long in 2000. The discrepancy between "apparent time" and "mean time" can add up to ~15 min. How does this come about?

The inclination of the ecliptic

First note that the Earth rotates on its axis not once in 24 h but once in 23 h 56 min 4 s. It's just that in the course of a year, the Earth must turn 366 times on its axis for the Sun to rise and set 365 times. To gain this extra turn, the sidereal day must be shorter than the solar day by one three-hundred-and-sixty-sixth:

<math>

\frac{1\ {\rm day}}{366} \times \frac{24\ {\rm h}}{1\ {\rm day}} \times \frac{60\ {\rm min}}{1\ {\rm h}} = 3\ {\rm min}\ 56\ {\rm s} <math>

The trouble comes in because this 3 min 56 s is only a yearly average value. Think of an observer sitting at the north pole on a platform which rotates once every 23 h 56 min 4 s so as to compensate for the Earth's rotation. The observer will see the stars as stationary and the Sun as moving in a circle. The plane of this circle is called the ecliptic and is tilted by 23.44° relative to the equatorial plane. Over the course of a year, the observer will see the Sun move from the horizon (which is parallel to the equatorial plane), up to an altitude of 23.44°, back down to the horizon, then down to an altitude of -23.44° (below the horizon). The Sun will move at a constant speed (this is not quite true, but wait till later) along its circle, but the shadow cast by the North Pole (if a physical pole were there) will not move at a constant rate. When the Sun is rising or setting, it is climbing/lowering at a 23.44° angle, so that it has to move 1.09° before the shadow moves 1°.

<math>

\frac{1^\circ}{\cos 23.44^\circ } = 1.0899^\circ\, <math>

On the other hand, in the middle of summer or winter, the Sun is high/low in the sky taking a short cut across meridians, so it must move only 1° along its circle to cause the shadow to move 1.09°. The cycle occurs twice per year and is independent of the observer's latitude, so that in spring and fall the 3 min 56 s is reduced by the factor 1.09 to 3 min 37 s, whereas in summer and winter it is correspondingly increased to 4 min 17 s. Thus a sundial can gain or lose up to 20.3 s/day due to the inclination of the ecliptic, depending on the time of year. If it is accurate on one day, a month and a half later it will have accumulated the maximum error of 9.8 min.

The seasonal correction is known as the "equation of time" and must obviously be taken into account if we want our sundial to be exact to the minute. If the gnomon (the shadow casting object) is not an edge but a point (e.g., a hole in a plate), the shadow (or spot of light) will trace out a curve during the course of a day. If the shadow is cast on a plane surface, this curve will (usually) be a hyperbola, since the circle of the Sun's motion together with the gnomon point define a cone, and a plane intersects a cone in a conic section (hyperbola, parabola, ellipse, or circle). At the spring and fall equinoxes, the cone degenerates to a plane and the hyperbola to a line. With a different hyperbola for each day, hour marks can be put on each hyperbola which include any necessary corrections. Unfortunately, each hyperbola corresponds to two different days, one in each half of the year, and these two days will require different corrections. A convenient compromise is to draw the line for the "mean time" and add a curve showing the exact position of the shadow points at noon during the course of the year. This curve will take the form of a figure eight and is known as an "analemma". By comparing the analemma to the mean noon line, the amount of correction to be applied generally on that day can be determined. At the equinoxes, it so happens that the solar day is closer to the sidereal day than on average (that is, it is shorter), so the sundial is running fast. This means in fall and spring the correct time will be earlier than the shadow indicates, by an amount given by the curve. In summer and winter the correct time will be later than indicated.

The eccentricity of the Earth's orbit

If you look at such a figure eight calculated correctly, you will see that the fall and winter loop is actually somewhat larger than the spring and summer loop. This is due to the slight inaccuracy mentioned above. The Earth does not actually orbit at a constant speed around the Sun. On January 3–4, the Earth is at its perihelion, 1.67% closer to the Sun than on average and thus its angular velocity is 3.37% larger (conservation of angular momentum). This makes the solar day on that date longer than the sidereal day by about 7.9 s more than on average,

<math>

\frac{3\ {\rm min}\ 56\ {\rm s}}{1\ {\rm day}} \times 0.0337 = 7.9\ {\rm s/day} <math>

and in the course of three months (thirteen weeks) a sundial accumulates an error of 7.6 min due to the eccentricity of the Earth's orbit. The cycle occurs once per year (in fact, it takes slightly more than a year to complete because of the slow precession of the Earth's perihelion).

Thus the correct time will be later than the shadow indicates at the spring equinox and earlier at the fall equinox. This shifts the dates at which the sundial is exactly right from the equinoxes into the summer, making the summer loop of the figure eight smaller. The 20.3 s/day error due to the inclination of the ecliptic and the 7.9 s/day error due to the eccentricity work in the same direction just before Christmas (around December 21) and add up almost exactly to the 30 s/day mentioned earlier. The accumulated errors of 9.8 min and 7.6 min due to these two effects don't add up quite so neatly, so the maximum accumulated error turns out to be somewhat less than 17 min. If you calculate everything correctly, you find that during the course of a year a sundial will be up to 16 min 33 s fast (on October 31–November 1) and up to 14 min 20 s slow (on February 12–13). Suppose in October you start a 15 min coffee break at 10:45 by the wall clock. If you believe the sundial outside, without accounting for the equation of time you will already be late for the 11:00 session as soon as you step out the door.

More details

The equation of time is the sum of two offset sine curves, with periods of one year and six months respectively. It can be approximated by

where

<math>B = 360^\circ (N - 81) / 364 \,<math> if sin and cos operate on degrees.

<math>B = 2\pi (N - 81) / 364 \,<math> if sin and cos operate on radians.

<math>N<math> is the so-called day number, i.e.,

<math>N=1<math> for January 1

<math>N=2<math> for January 2

and so on.

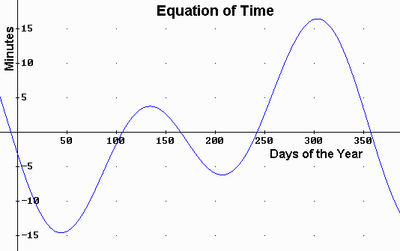
The following is a graph of the current equation of time. Positive values mean the sundial is ahead of mean time, negative means it is behind. The form can vary over the course of many centuries.