Transverse wave
|
|
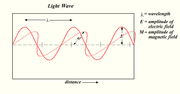
A transverse wave is a wave that oscillates perpendicular to the direction it advances. For example: if a wave moves along the x-axis, its oscillations are in the y-z plane. In other words, it oscillates across the 2-dimensional plane that it is travelling in. It may oscillate either vertically or horizontally, and this refers to its polarity. Electromagnetic waves are transverse waves. Imagine a slinky spread across a table. If you move it to the left and right or if you move it up and down it would represent a transverse wave. Oscillating string is maybe the simplest example for transverse wave.
Transverse waves travel slower than longitudinal waves (which include sound, ripples in water, and certain types of waves from earthquakes, where the particle motion is in the direction of travel), and propagate only in solids, not in liquids or gases. In seismology transverse waves are called S (for “secondary”) waves as they arrive later than the P (“primary”) waves from an earthquake. The absence of transverse waves traveling through the earth’s core shows that it is liquid.
In mathematics, transverse waves are associated with the curl operator and are governed by a vector wave equation, in contrast to longitudinal waves, which are associated with the div operator and are governed by a scalar wave equation. A longitudinal wave exists as compressions moving through the plane in which it is travelling. Energy from this wave is transmitted as mechanical energy. An example would be a slinky which was pushed forward and backwards, compressing and extending it as the motion of the wave was transmitted.
Light is composed of transverse waves. See electromagnetic spectrum for information on different types of electromagnetic waves.
