Snell's law
|
|
Snell's law is the simple formula used to calculate the refraction of light when travelling between two media of differing refractive index. It is named for its discoverer, Dutch mathematician Willebrord van Roijen Snell (1580-1626).
| Contents |
Overview
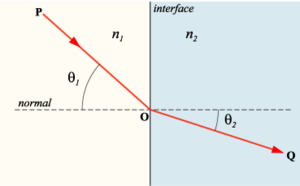
In the diagram on the right, two media of refractive indices n1 (on the left) and n2 (on the right) meet at a surface or interface (vertical line). n2 > n1, and light has a slower phase velocity within the second medium.
A light ray PO in the leftmost medium strikes the interface at the point O. From point O, we project a straight line at right angles to the line of the interface; this is known as the normal to the surface (horizontal line). The angle between the normal and the light ray PO is known as the angle of incidence, θ1.
The ray continues through the interface into the medium on the right; this is shown as the ray OQ. The angle with which is makes to the normal is known of as the angle of refraction, θ2.
Snell's law gives the relation between the angles θ1 and θ2:
- <math>n_1\sin(\theta_1) = n_2\sin(\theta_2)\, <math>
Note that, for the case of θ1 = 0° (i.e., a ray perpendicular to the interface) the solution is θ2 = 0° regardless of the values of n1 and n2. In other words, a ray entering a medium perpendicular to the surface is never bent.
The above is also valid for light going from a dense to a less dense medium; the symmetry of Snell's law shows that the same raypaths are applicable in opposite direction.
A qualitative rule for determining the direction of refraction is that the ray in the denser medium is always closer to the normal. A handy way to remember this is to visualize the ray as a car crossing the boundary between asphalt (the less dense medium) and mud (the denser medium). Depending on the angle, either the left wheel or the right wheel of the car will cross into the new medium first, causing the car to swerve.
Total internal reflection
When moving from a dense to a less dense medium (i.e. n1 > n2), it is easily verified that the above equation has no solution when θ1 exceeds a value known as the critical angle:
- <math>\theta_{\mathrm{crit}} = \sin^{-1}\left( \frac{n_2}{n_1} \right)<math>
When θ1 > θcrit, no refracted ray appears, and the incident ray undergoes total internal reflection from the interface.
Given a normalized ray vector v and a normalized plane normal vector p, one can work out the normalized reflected and refracted rays: (note that the actual angles θ1 and θ2 are not worked out)
- <math>\cos\theta_1=\mathbf{v}\cdot\mathbf{p}<math>
- <math>\cos\theta_2=\sqrt{1-\left(\frac{n_1}{n_2}\right)^2\left(1-\left(\cos\theta_1\right)^2\right)}<math>
- <math>\mathbf{v}_{\mathrm{reflect}}=\mathbf{v}-\left(2\cos\theta_1\right)\mathbf{p}<math>
- <math>\mathbf{v}_{\mathrm{refract}}=\left(\frac{n_1}{n_2}\right)\mathbf{v}+\left(\cos\theta_2-\frac{n_1}{n_2}\cos\theta_1\right)\mathbf{p}<math>
The cosines may be recycled and used in the Fresnel equations for working out the intensity of the resulting rays. The square root turns imaginary during total internal reflection, and the refracted ray is not real (there is apparently some kind of refracted ray, which decays very quickly, exponentially with distance).
Derivation
Snell's law may be derived from Fermat's principle, which states that the light travels the path which takes the least time. By taking the derivative of the optical path length, the stationary point is found giving the path taken by the light. In a classic analogy by Feynman, the area of lower refractive index is replaced by a beach, the area of higher refractive index by the sea, and the fastest way for a rescuer on the beach to get to a drowning person in the sea is to run along a path that follows Snell's law.
History
Snell's law seems to have been discovered first by Ibn Sahl in the 10th century, who used it to work out the shapes of anaclastic lenses (lenses that focus light with no geometric aberrations). It was discovered again by Thomas Harriot in the late 16th century. In the 17th century, it was discovered yet another time, by either Willebrord Snell or René Descartes, but the priority of the discoverer is fraught, and not completely clear. In his publication of the law, Descartes used it to solve a range of optical problems and, in French, Snell's Law is called "la loi de Descartes".
Related topics
External links
- Discovery of the law of refraction (http://mintaka.sdsu.edu/GF/explain/optics/discovery.html)de:Snelliussches Brechungsgesetz
es:Ley de Snell fr:Loi de Snell-Descartes ja:スネルの法則 nl:Wet van Snellius sl:lomni zakon sv:Snells lag zh:光的折射定律