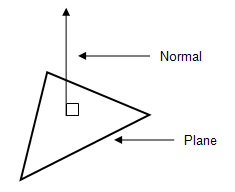
Surface normal
|
|
A surface normal, or just normal to a flat surface is a three-dimensional vector which is perpendicular to that surface. A normal to a non-flat surface at a point p on the surface is a vector which is perpendicular to the tangent plane to that surface at p.
Calculating the surface normal
For a polygon (such as a triangle), a surface normal can be calculated as the vector cross product of two edges of the polygon.
For a plane given by the equation <math>ax+by+cz=d<math>, the vector <math>(a, b, c)<math> is a normal.
If a (possibly non-flat) surface S is parametrized by a system of curvilinear coordinates x(s, t), with s and t real variables, then a normal is given by the cross product of the partial derivatives
- <math>{\partial \mathbf{x} \over \partial s}\times {\partial \mathbf{x} \over \partial t}.<math>
If a surface S is given implicitly, as the set of points <math>(x, y, z)<math> satisfying <math>F(x, y, z)=0<math>, then, a normal at a point <math>(x, y, z)<math> on the surface is given by the gradient
- <math>\nabla F(x, y, z).<math>
If a surface does not have a tangent plane at a point, it does not have a normal at that point either. For example, a cone does not have a normal at its tip.
Uses
- Surface normals are essential in defining surface integrals of vector fields.
- Surface normals are commonly used in 3D computer graphics for lighting calculations, see Lambert's cosine law.
External link
- An explanation of normal vectors (http://msdn.microsoft.com/library/default.asp?url=/library/en-us/directx9_c/directx/graphics/programmingguide/GettingStarted/3DCoordinateSystems/facevertexnormalvectors.asp) from Microsoft's MSDNcs:Normála