Projective plane

In mathematics, a projective plane consists of a set of "lines" and a set of "points" with the following properties:

The last condition simply excludes some degenerate cases (see below).

Note that a projective plane is an abstract mathematical concept, so the "lines" need not be anything resembling ordinary lines, nor need the "points" resemble ordinary points. The most common projective plane is the real projective plane, which is a topological surface with surprising geometric properties; after that is the complex projective plane of algebraic geometry, a topological four-dimensional manifold.

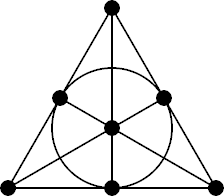The smallest possible projective plane has only seven points and seven lines. It is often called the Fano plane, and is shown in the picture on the right. In this representation of the Fano plane, the seven points are shown as small black balls, and the seven lines are shown as six line segments and a circle. However, we could equally consider the balls to be the "lines" and the line segments and circle to be the "points" — this is an example of the duality of projective planes: if the lines and points are interchanged, the result is still a projective plane.

It can be shown that a projective plane has the same number of lines as it has points. This number can be infinite (as for the real projective plane) or finite (as for the Fano plane). A finite projective plane has n² + n + 1 points, where n is an integer called the order of the projective plane. (The Fano plane therefore has order 2.) For all known finite projective planes, the order n is a prime power. The existence of finite projective planes of other orders is an open question. The only general restriction known on the order is the Bruck-Ryser-Chowla theorem that if the order n is congruent to 1 or 2 mod 4, it must be the sum of two squares. This rules out n = 6. The next case n = 10 has been ruled out by massive computer calculations, and there is nothing more known, in particular n = 12 is still open. A projective plane of order n has n + 1 points on every line, and n + 1 lines passing through every point, and is therefore a Steiner S(2, n +1, n² + n + 1) system (see Steiner system).

One can construct projective planes or higher dimensional projective spaces by linear algebra over any division ring - not necessarily commutative. If we use a finite field with pⁿ elements we get a finite projective plane with order pⁿ. The Fano plane is then the plane over the field with two elements, Z₂. One can also do the reverse, and construct a coordinate "ring" - a so-called Planar Ternary Ring (not necessarily a genuine ring) corresponding to any projective plane as defined above. Algebraic properties of this "ring" turn out to correspond to geometric incidence properties of the plane. For example, Desargues' theorem corresponds to the coordinate ring being a division ring, while Pappus's theorem corresponds to this ring being commutative. However, the "ring" need not be of this type, and there are many non-Desarguesian projective planes. Alternative, not necessarily associative division rings correspond to Moufang planes. In the case of finite projective planes, the only proof known of the purely geometric statement that Desargues theorem then implies Pappus' theorem (the converse being always true and provable geometrically) is through this algebraic route, using Wedderburn's theorem that finite division rings must be commutative.

It is possible to make analogous incidence definitions for higher dimensional projective n-spaces, for n larger than 2. These turn out to not be as interesting as the planar case, as they correspond to classical projective geometry over division rings for a very simple reason: with the extra room to work in, one can prove Desargues theorem geometrically as in its article by using incidence properties in this higher dimensional space and thus the coordinate "ring" must be a division ring.

The plane over the octonions turns out to be an interesting real manifold, which can be used for geometric constructions and understanding of the Exceptional Lie groups.

Contents

1 Degenerate planes 2 Construction of projective planes of prime order 3 See also 4 External links 5 References

Degenerate planes

Degenerate planes do not fulfill the third condition above. There are two families of degenerate planes.

1) For any number of points P₁, ..., P_n, and lines L₁, ..., L_m,

L₁ = { P₁, P₂, ..., P_n}

L₂ = { P₁ }

L₃ = { P₁ }

...

L_m = { P₁ }

2) For any number of points P₁, ..., P_n, and lines L₁, ..., L_n, (same number of points as lines)

L₁ = { P₁, P₂, P₃, ..., P_n }

L₂ = { P₁, P₂ }

L₃ = { P₁, P₃ }

...

L_n = { P₁, P_n }

Construction of projective planes of prime order

To construct a projective plane of order N (N prime), proceed as follows:

Create N² points, which we will label P(r, c) : r, c = 0, ..., (N − 1)

Create N points, which we will label P(c) : c = 0, ..., (N − 1)

Create one point P

On these points, construct the following lines:

One line L = { P, P(0), ..., P(N − 1)}

N lines L(c) = {P, P(0,c), ..., P(N − 1,c)} : c = 0, ..., (N − 1)

N² lines L(r, c): { P(c), P((r + ci) mod N, i) } : r, c = 0, ..., (N − 1)

Note that the expression

(r + ci) mod N

will pass once through each value as i varies from 0 to N − 1, but only if is N is prime.

By this construction, we have two degenerate planes: one point incident with one line (for N = 0) and a triangle consisting of three points and three lines (for N = 1). Every plane constructed with prime N (N > 1) fulfills all three conditions above.

See also

• Incidence structure
• Projective geometry

External links

• Projective plane on mathworld (http://mathworld.wolfram.com/ProjectivePlane.html)
• Lam, Clement W.H. (1996). "The Search for a Finite Projective Plane of Order 10" (http://www.cecm.sfu.ca/organics/papers/lam/). Retrieved Apr. 30, 2005.

References

• Template:Book reference