Incidence structure
|
|
| Contents |
Definition
In mathematics, in particular in combinatorics, an incidence structure is a triple
- <math>C=(P,L,I)<math>
where <math>P<math> is the set of "points", <math>L<math> is the set of "lines" and <math>I \subseteq P \times L<math> is the incidence relation. The elements of <math>I<math> are called flags. If <math>(p,l) \in L<math> we say that "point" <math>p<math> lies on "line" <math>l<math>.
Dual structure
If we interchange the role of "points" and "lines" in
- <math>C=(P,L,I)<math>
the dual structure
- <math>C^*=(L,P,I^*)<math>
is obtained. Clearly
- <math>C^{**}=C.<math>
A structure <math>C<math> that is isomorphic to its dual <math>C^*<math> is called self-dual.
Hypergraphs as incidence structures
Each hypergraph or set system can be regarded as an incidence structure in which the universal set plays the role of "points", the corresponding family of sets plays the role of "lines" and the incidence relation is given by <math>\in<math>.
Example: Fano plane
In particular, let
- P = {1,2,3,4,5,6,7},
- L = {{1,2,4},{2,3,5},{3,4,6},{4,5,7},{5,6,1},{6,7,2},{7,1,3}}
- <math>I = \in<math>.
The corresponding incidence structure is called the Fano plane.
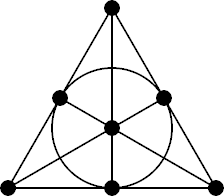
Geometric representation
Incidence structures can be modelled by points and curves in the Euclidean plane with usual geometric incidence. Some incidence structures admit representation by points and lines. Fano plane is not one of them since it needs at least one curve.
Incidence structure and its Levi graph
To each incidence structure <math>C<math> we may associate a bipartite graph called Levi graph or incidence graph with a given black and white vertex coloring where black vertices correspond to points and white vertices correspond to lines of <math>C<math> and the edges correspond to flags.
Example (revisited)
Missing image
Heawood.jpg
Image:Heawood.jpg
For instance, the Levi graph of the Fano plane is the Heawood graph. Since the Heawood graph is connected and vertex-transitive, it follows that there exists an automorphism (such as the one defined by a reflection about the vertical axis in the above figure) interchanging black and white vertices. This, in turn, implies that the Fano plane is self-dual.
