Normal mode
|
|
Normal modes in an oscillating system are special solutions where all the parts of the system are oscillating with the same frequency (called normal frequencies or allowed frequencies). The concept of normal modes is of vital importance in wave theory, optics and quantum mechanics.
Finding normal modes in harmonic oscillation uses the strength of linear algebra and linear sets of differential equations. One can present the problem as a matrix-vector equation and then solve for its eigenvectors. After finding them, the normal modes are the eigenvectors where the normal frequencies are the eigenvalues.
| Contents |
Example - normal modes of coupled oscillators
Consider two bodies (not affected by gravity), each of mass M, attached to three springs with stiffness K. They are attached in the following manner:
- Missing image
Two_masses.png
Image:Two masses.png
where the edge points are fixed and cannot move. We'll use x1(t) to denote the displacement of the leftmost mass, and x2(t) to denote the displacement of the rightmost.
If we denote the second derivative of x(t) with respect to time as x″, the equations of motion are:
- <math>
M \cdot x_1'' = - K \cdot (x_1) - K \cdot (x_1 - x_2) <math>
- <math>
M \cdot x_2'' = - K \cdot (x_2) - K \cdot (x_2 - x_1) <math>
And in matrix representation:
- <math>
\begin{pmatrix} x_1'' \\ x_2'' \end{pmatrix} = (K/M)\cdot \begin{bmatrix} -2 & 1 \\ 1 & -2 \end{bmatrix} \begin{pmatrix} x_1 \\ x_2 \end{pmatrix} <math>
For simplicity of writing lets assume that (K/M) = 1. Note that this "1" has a units of square frequency. In a normal mode the solution satisfy:
- <math>
\begin{pmatrix} x_1'' \\ x_2'' \end{pmatrix} = -(\omega)^2\cdot \begin{pmatrix} x_1 \\ x_2 \end{pmatrix} <math>
Or:
- <math>
0 = \begin{bmatrix} (\omega)^2-2 & 1 \\ 1 & -2 + (\omega)^2 \end{bmatrix} \begin{pmatrix} x_1 \\ x_2 \end{pmatrix} <math>
Demanding that a non-trivial solution exists, i.e the determinant is equal to 0 leads for solving the characteristic polynomial, we obtain:
- <math>
\begin{pmatrix} 1 \\ 1 \end{pmatrix} \quad ; \quad (\omega^2)_1 = 1 <math>
- <math>
\begin{pmatrix} 1 \\ -1 \end{pmatrix} \quad ; \quad (\omega^2)_2 = 3 <math>
The left vector is the eigenvector and the right scalar is the normal frequency.
The first normal mode is:
- <math>
\begin{pmatrix} x_1(t) \\ x_2(t) \end{pmatrix} = c_1 \cdot \begin{pmatrix} 1 \\ 1 \end{pmatrix} \cdot \cos{(t + \phi_1)} <math>
and the second normal mode is:
- <math>
\begin{pmatrix} x_1(t) \\ x_2(t) \end{pmatrix} = c_2 \cdot \begin{pmatrix} 1 \\ -1 \end{pmatrix} \cdot \cos{(\sqrt3 \cdot t + \phi_2)}
<math>
The general solution is a superposition of the normal modes where c1, c2, φ1, and φ1, are determined by the initial conditions of the problem.
The process demonstrated here can be generalized and formulated using the formalism of Lagrangian mechanics or Hamiltonian mechanics.
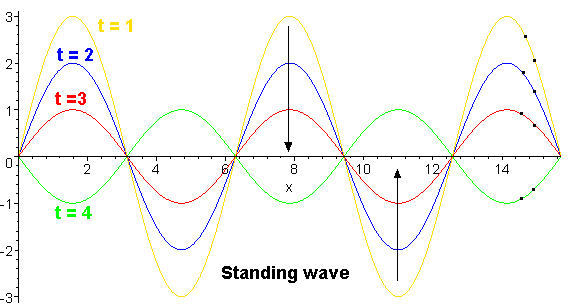
Standing waves
A standing wave is a continuous form of normal mode. In a standing wave, all the space elements (i.e (x,y,z) coordinates) are oscillating in the same frequency and in phase (reaching the equilibrium point together), but each has a different amplitude.
The general form of a standing wave is:
- <math>
\Psi(t) = f(x,y,z) \cdot (A\cos(\omega \cdot t) + B\sin(\omega \cdot t)) <math>
where f(x,y,z) represents the dependence of amplitude on location and the cosine\sine are the oscillations in time.
Physically, standing waves are formed by the interference (superposition) of waves and their reflections (although one may also say the opposite; that a moving wave is a superposition of standing waves). The geometric shape of the medium determines what would be the interference pattern, thus determines the f(x,y,z) form of the standing wave. This space-dependence is called a normal mode.
Usually, for problems with continuous dependence on (x,y,z) there is no single or finite number of normal mode, but there are infinitely normal modes. If the problem is bounded (i.e it is defined on a finite section of space) there are countably many (a discrete infinity of ) normal modes (usually numbered n = 1,2,3,...). If the problem is not bounded, there is a continuous spectrum of normal modes.
The allowed frequencies are dependent on the normal modes, as well on physical constants of the problem (density, tension, pressure, etc.) which sets the phase velocity of the wave. The range of all possible normal frequencies is called the frequency spectrum. Usually, each frequency is modulated by the amplitude at which it has arisen, creating a graph of the power spectrum of the oscillations.
When relating to music, normal modes of a vibrating instruments (strings, air pipes, drums, etc.) are called "harmonics".
Normal modes in quantum mechanics
In quantum mechanics, a state of a system is described by a wavefunction <math>\ | \psi \rang<math> of (x, t) which solves the Schrödinger equation. The square of the absolute value of <math>\ | \psi \rang <math> ,i.e.
- <math>
\ P(x,t) = |\psi (x,t)|^2 <math>
is the probability (density) to measure the particle in place x at time t.
Usually, when involving some sort of potential, the wavefunction is decomposed into a superposition of energy eigenstates, each oscillating with frequency of <math> \omega = E_n / \hbar <math>. Thus, we may write
- <math>
|\psi (t) \rang = \sum_n |n\rang \left\langle n | \psi ( t=0) \right\rangle e^{-iE_nt/\hbar} <math>
The eigenstates have a physical meaning further than an orthonormal basis. When a measurement takes place, the wavefunction collapses into one of its eigenstates and so the particle wavefunction is described only by the eigenstate corresponding to the measured energy.
See also
- Physical applications:
- Mathematical tools:
External links
- Java simulation of coupled oscillators (http://www.falstad.com/coupled/).
- Java simulation of the normal modes of a string (http://www.falstad.com/loadedstring/), drum (http://www.falstad.com/circosc/), and bar (http://www.falstad.com/barwaves/).