Logic gate
|
|
A logic gate is an arrangement of switches used to calculate operations in Boolean algebra.
| Contents |
Electronic gates
Logic gates are primarily electronically-controlled but can also be constructed from electromagnetic relays, electronic diodes, fluidics, optical or even mechanical elements.
Logic gates built from relays and switches
While semiconductor electronic logic (see later) is preferred in most applications, relays and switches are still used in some industrial applications and for educational purposes. In this article, the various types of logic gate are illustrated with drawings of their relay-and-switch implementations, although the reader should remember that these are electrically different from the semiconductor equivalents that are discussed later.
Relay logic was historically important in industrial automation (see ladder logic and programmable logic controller). Since relay contacts conduct in both directions, complex logic designs must be checked for "sneak paths" that produce unintended logic paths.
| INPUT | OUTPUT | |
|---|---|---|
| A | B | A AND B |
| 0 | 0 | 0 |
| 1 | 0 | 0 |
| 0 | 1 | 0 |
| 1 | 1 | 1 |
Circuit_and.png
Switch circuit diagram for AND gate
The first example is the AND gate, whose truth table is shown opposite.
The Boolean AND function can be implemented with two switches, A and B, as shown opposite. A power lead is connected to one switch, and a wire is connected between the two, such that both A and B have to be "on" in order for the circuit to conduct electricity.
| INPUT | OUTPUT | |
|---|---|---|
| A | B | A OR B |
| 0 | 0 | 0 |
| 1 | 0 | 1 |
| 0 | 1 | 1 |
| 1 | 1 | 1 |
Another important arrangement is the OR gate, whose truth table is shown opposite.
An OR gate can be constructed from two switches, arranged so that if either switch is "on", the output will also be "on".
| INPUT | OUTPUT |
|---|---|
| A | NOT A |
| 0 | 1 |
| 1 | 0 |
Switch_circuit_not.png
Switch circuit diagram for NOT gate
A simpler arrangement is the NOT gate, whose truth table is shown opposite.
This is a special switch that when pushed breaks the current when it is pressed. The normally-closed contact of a relay can be used for this purpose.
Using NOT gates, also called inverters, allows us to make alternate versions of the AND and OR gates, by virtue of De Morgan's Law. Note that the layout of the switches in the two circuits is swapped when we turn the switches "backwards". Also note how the output of the first pair controls the operation of the NOT gate.
Switch_alternate_and_or.png
Switch diagram of alternate AND and OR gates
This may seem like an unnecessary complication, but in fact this is very useful. By removing the NOT gate from these alternate circuits, we create the so-called NAND (for NOT-AND) and NOR (for NOT-OR) gates.
The preceding simple logic gates can be combined to form more complicated boolean logic circuits. Logic circuits are often classified in two groups: combinatorial logic, in which the outputs are continuous-time functions of the inputs, and sequential logic, in which the outputs depend on information stored by the circuit as well as on the inputs.
Logic Gates
The simplest form of electronic logic is diode logic. This allows AND and OR gates to be built, but not inverters, and so is an incomplete form of logic. To build a complete logic system, valves or transistors can be used. The simplest family of logic gates using bipolar transistors is called resistor-transistor logic, or RTL. Unlike diode logic gates, RTL gates can be cascaded indefinitely to produce more complex logic functions. These gates were used in early integrated circuits. For higher speed, the resistors used in RTL were replaced by diodes, leading to diode-transistor logic, or DTL. It was then discovered that one transistor could do the job of two diodes in the space of one diode, so transistor-transistor logic, or TTL, was created. In some types of chip, to reduce size and power consumption still further, the bipolar transistors were replaced with complementary field-effect transistors (MOSFETs), resulting in complementary metal-oxide-semiconductor (CMOS) logic.
For small-scale logic, designers now use prefabricated logic gates from families of devices such as the TTL 7400 series invented by Texas Instruments and the CMOS 4000 series invented by RCA, and their more recent descendants. These devices usually contain transistors with multiple emitters, used to implement the AND function, which are not available as separate components. Increasingly, these fixed-function logic gates are being replaced by programmable logic devices, which allow designers to pack a huge number of mixed logic gates into a single integrated circuit. The field-programmable nature of programmable logic devices such as FPGAs has removed the 'hard' property of hardware; it is now possible to change the logic design of a hardware system by reprogramming some of its components, thus allowing the features or function of a hardware implementation of a logic system to be changed.
Electronic logic gates differ significantly from their relay-and-switch equivalents. They are much faster, consume much less power, and are much smaller (all by a factor of a million or more in most cases). Also, there is a fundamental structural difference. The switch circuit creates a continuous metallic path for current to flow (in either direction) between its input and its output. The semiconductor logic gate, on the other hand, acts as a high-gain voltage amplifier, which sinks a tiny current at its input and produces a low-impedance voltage at its output. It is not possible for current to flow between the output and the input of a semiconductor logic gate.
Another important advantage of standardised semiconductor logic gates, such as the 7400 and 4000 families, is that they are cascadable. This means that the output of one gate can be wired to the inputs of one or several other gates, and so on ad infinitum, enabling the construction of circuits of arbitrary complexity without requiring the designer to understand the internal workings of the gates.
In practice, the output of one gate can only drive a finite number of inputs to other gates, a number called the 'fanout limit', but this limit is rarely reached in the newer CMOS logic circuits, as compared to TTL circuits. Also, there is always a delay, called the 'propagation delay', from a change an input of a gate to the corresponding change in its output. When gates are cascaded, the total propagation delay is approximately the sum of the individual delays, an effect which can become a problem in high-speed circuits.
The US symbol for an AND gate is: 
and the IEC symbol is Missing image
Iec_and.png
AND symbol
.
The US circuit symbol for an OR gate is: Missing image
Or-gate.png
OR symbol
and the IEC symbol is: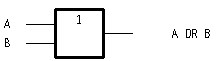 
(Symbol: ≥1).
The US circuit symbol for a NOT gate is: Missing image
Not-gate.png
NOT symbol
and the IEC symbol is: Missing image
Iec_not.png
NOT symbol
.
In electronics a NOT gate is more commonly called an inverter. The circle on the symbol is called a bubble, and is generally used in circuit diagrams to indicate an inverted input or output.
The US circuit symbol for a NAND gate is: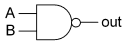 
and the IEC symbol is: Missing image
Iec_nand.png
NAND symbol
.
The US circuit symbol for a NOR gate is: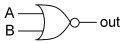 
and the IEC symbol is: 
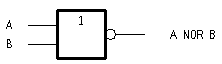(Symbol: ≥1).
In practice, the cheapest gate to manufacture is usually the NAND gate. Additionally, Charles Peirce showed that NAND gates alone (as well as NOR gates alone) can be used to reproduce all the other logic gates.
Two more gates are the exclusive-OR or XOR function and its inverse, exclusive-NOR or XNOR. Exclusive-OR is true only when exactly one of its inputs is true. In practice, these gates are built from combinations of simpler logic gates.
The US circuit symbol for an XOR gate is: Missing image
Xor-gate.png
XOR symbol
and the IEC symbol is: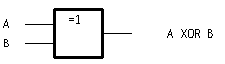 
.
Storage of bits
Related to the concept of logic gates (and also built from them) is the idea of storing a bit of information. The gates discussed up to here cannot store a value: when the inputs change, the outputs immediately react. It is possible to make a storage element either through a capacitor (which stores charge due to its physical properties) or by feedback. Connecting the output of a gate to the input causes it to be put through the logic again, and choosing the feedback correctly allows it to be preserved or modified through the use of other inputs. A set of gates arranged in this fashion is known as a "latch", and more complicated designs that utilise clocks (signals that oscillate with a known period) and change only on the rising edge are called edge-triggered "flip-flops". The combination of multiple flip-flops in parallel, to store a multiple-bit value, is known as a register.
These registers or capacitor-based circuits are known as computer memory. They vary in performance, based on factors of speed, complexity, and reliability of storage, and many different types of designs are used based on the application.
Three-state logic gates
Three-state, or 3-state, logic gates are a form of electronic logic gate in which the output has three possible states: high (H), low (L) and high-impedance (Z). The Z state exists merely to help the circuit designer and, unlike the H and L states, carries no information. This feature is used in circuits that have two or more logic outputs connected to a single logic input. A control circuit enables one output at a time depending on the logic function that is required, the other outputs being held in the Z state (also called 'disabled').
'Tri-state', a widely-used synonym of 'three-state', is a trademark of the National Semiconductor Corporation.
Miscellaneous
Logic circuits include such devices as multiplexers, registers, ALUs, and computer memory, all the way up through complete microprocessors which can contain more than a million gates. In practice, the gates are made from field effect transistors (FETs), particularly metal-oxide-semiconductor FETs (MOSFETs).
In reversible logic, Toffoli gates are used.
History and development
The earliest logic gates were made mechanically. Charles Babbage, around 1837, devised the Analytical Engine. His logic gates relied on mechanical gearing to perform operations. Electromagnetic relays were later used for logic gates. Almon Strowger patented, in 1891, a simple logic gate switch circuit, (Template:US patent). Strowger's patent was not in widespread use until the 1920s. Eventually, vacuum tubes replaced relays for logic operations. Lee De Forest's modification, in 1907, of the Fleming valve can be used as AND logic gate. Claude E. Shannon introduced the use of Boolean algebra in the analysis and design of switching circuits in 1937. Walther Bothe, inventor of the coincidence circuit, got part of the 1954 Nobel prize in physics, for the first modern electronic AND gate in 1924.
See also
- Digital circuit
- Digital logic
- Fanout
- Karnaugh map
- List of Boolean algebra topics
- Families of logic devices
- NMOS
- Race hazard
- Sheffer stroke
- Venn diagram
External links and references
- Tesla's invention of the AND logic gate (http://www.tfcbooks.com/teslafaq/q&a_024.htm). Twenty First Century Books, Breckenridge, CO.
- Wireless Remote Control and the Electronic Computer Logic Gate (http://www.tfcbooks.com/articles/control.htm). Twenty First Century Books, Breckenridge, CO.
- Anderson, Leland I., "Nikola Tesla — Guided Weapons & Computer Technology". ISBN 0-9636012-5-3
- Bigelow, Ken, "How logic gates work internally (for several logic families) (http://www.play-hookey.com/digital/electronics/)", play-hookey.com.
- C. E. Shannon, "A symbolic analysis of relay and switching circuits," Transactions American Institute of Electrical Engineers, vol. 57, pp. 713-723, March 1938.
- The IEC symbols are defined in IEC 60617-12 (1997-12), Graphical symbols for diagrams - Part 12: Binary logic elements
- "Logic gate (http://www.sharpened.net/glossary/definition.php?logicgate)". Sharpened Productions, 2005.
- "LEGO Logic Gates (http://goldfish.ikaruga.co.uk/logic.html)". goldfish.org.uk, 2005.
Further reading
- Bostock, Geoff, "Programmable logic devices : technology and applications". New York, McGraw-Hill, c1988. ISBN 0070066116
- Brown, Stephen D. et. al., "Field-programmable gate arrays". Boston, Kluwer Academic Publishers, c1992. The Kluwer international series in engineering and computer science. ISBN 0792392485
- Awschalom, D., D. Loss, and N. Samarth, "Semiconductor spintronics and quantum computation". Berlin, Springer, c2002. ISBN 3540421769
da:Gate (digital elektronik) de:Gatter (Elektronik) es:Puerta lógica fr:Fonction logique he:שער לוגי nl:Logische poort pl:Bramka logiczna sr:Логичка капија zh:邏輯門