List of small groups
|
|
The following list in mathematics contains the finite groups of small order up to group isomorphism.
The list can be used to determine which known group a given finite group G is isomorphic to: first determine the order of G, then look up the candidates for that order in the list below. If you know whether G is abelian or not, some candidates can be eliminated right away. To distinguish between the remaining candidates, look at the orders of your group's elements, and match it with the orders of the candidate group's elements.
Glossary
- Cn: the cyclic group of order n.
- Dn: the dihedral group of order n.
- Sn: the symmetric group of degree n, containing the n! permutations of n elements.
- An: the alternating group of degree n, containing the n!/2 even permutations of n elements.
- Dicn: the dicyclic group of order 4n.
The notation G × H stands for the direct product of the two groups. Abelian and simple groups are noted. (For groups of order n < 60, the simple groups are precisely the cyclic groups Cn, where n is prime.) We use the equality sign ("=") to denote isomorphism.
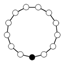
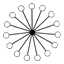
The identity element in the cycle graphs are represented by the black circle.
List
| Order | Group | Properties | Cycle graph |
|---|---|---|---|
| 1 | trivial group = C1 = S1 = A2 | abelian | Missing image GroupDiagramMiniC1.png |
| 2 | C2 = S2 | abelian, simple, the smallest non-trivial group | Missing image GroupDiagramMiniC2.png |
| 3 | C3 = A3 | abelian, simple | Missing image GroupDiagramMiniC3.png |
| 4 | C4 | abelian, | Missing image GroupDiagramMiniC4.png |
| Klein four-group = C2 × C2 = D4 | abelian, the smallest non-cyclic group | Missing image GroupDiagramMiniD4.png |
|
| 5 | C5 | abelian, simple | Missing image GroupDiagramMiniC5.png |
| 6 | C6 = C2 × C3 | abelian | Missing image GroupDiagramMiniC6.png |
| S3 = D6 | the smallest non-abelian group | Missing image GroupDiagramMiniD6.png |
|
| 7 | C7 | abelian, simple | Missing image GroupDiagramMiniC7.png |
| 8 | C8 | abelian | Missing image GroupDiagramMiniC8.png |
| C2 ×C4 | abelian | Missing image GroupDiagramMiniC2C4.png |
|
| C2 × C2 × C2 = D4 × C2 | abelian | Missing image GroupDiagramMiniC2x3.png |
|
| D8 | non-abelian |  |
|
| Quaternion group, Q8 = Dic2 | non-abelian; the smallest Hamiltonian group |  |
|
| 9 | C9 | abelian | Missing image GroupDiagramMiniC9.png |
| C3 × C3 | abelian | Missing image GroupDiagramMiniC3x2.png |
|
| 10 | C10 = C2 × C5 | abelian | Missing image GroupDiagramMiniC10.png |
| D10 | non-abelian | Missing image GroupDiagramMiniD10.png |
|
| 11 | C11 | abelian, simple | Missing image GroupDiagramMiniC11.png |
| 12 | C12 = C4 × C3 | abelian | Missing image GroupDiagramMiniC12.png |
| C2 × C6 = C2 × C2 × C3 = D4 × C3 | abelian | Missing image GroupDiagramMiniC2C6.png |
|
| D12 = D6 × C2 | non-abelian | Missing image GroupDiagramMiniD12.png |
|
| A4 | non-abelian | Missing image GroupDiagramMiniA4.png |
|
| Dic3 = the semidirect product of C3 and C4, where C4 acts on C3 by inversion | non-abelian | Missing image GroupDiagramMiniX12.png |
|
| 13 | C13 | abelian, simple |  |
| 14 | C14 = C2 × C7 | abelian | Missing image GroupDiagramMiniC14.png |
| D14 | non-abelian | Missing image GroupDiagramMiniD14.png |
|
| 15 | C15 = C3 × C5 | abelian | Missing image GroupDiagramMiniC15.png |
| 16 | C16 | abelian | Missing image GroupDiagramMiniC16.png |
| C2 × C2 × C2 × C2 | abelian |  |
|
| C2 × C2 × C4</sup> | abelian | Missing image GroupDiagramMiniC2x2C4.png |
|
| C2 × C8 | abelian | Missing image GroupDiagramMiniC2C8.png |
|
| C4 × C4 | abelian | Missing image GroupDiagramMiniC4x2.png |
|
| D16 | non-abelian | Missing image GroupDiagramMiniD16.png |
|
| Generalized quaternion group, Q16 = Dic4 | non-abelian | Missing image GroupDiagramMiniQ16.png |
|
| C2 × D8 | non-abelian | Missing image GroupDiagramMiniC2D8.png |
|
| C2 × Q8 | non-abelian | Missing image GroupDiagramMiniC2Q8.png |
|
| The order 16 quasidihedral group | non-abelian | Missing image GroupDiagramMiniQH16.png |
|
| The order 16 modular group | non-abelian | Missing image GroupDiagramMiniMOD16.png |
|
| The semidirect product of C4 and C4 where one factor acts on the other by inversion | non-abelian | Missing image GroupDiagramMinix3.png |
|
| The group generated by the Pauli matrices | non-abelian | Missing image GroupDiagramMiniPauli.png |
|
| G4,4 | non-abelian | Missing image GroupDiagramMiniG44.png |