Lambert's W function
|
|
In mathematics, Lambert's W function, named after Johann Heinrich Lambert, also called the Omega function, is the inverse function of
- <math>f(w) = w e^w\,<math>
where ew is the exponential function and w is any complex number. Lambert's function is usually denoted W(z). For every complex number z, we have
- <math>z = W(z)e^{W(z)}\,<math>
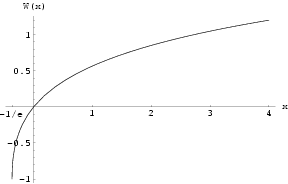
Since the function f is not injective in (−∞, 0), the function W is multivalued in [−1/e, 0). If we restrict to real arguments x ≥ −1/e and demand w ≥ −1, then a single-valued function W0(x) is defined, whose graph is shown. We have W0(0) = 0 and W0(−1/e) = −1.
The Lambert W function cannot be expressed in terms of elementary functions. It is useful in combinatorics, for instance in the enumeration of trees. It can be used to solve various equations involving exponentials and also occurs in the solution of time-delayed differential equations, such as y'(t) = a y(t − 1).
By implicit differentiation, one can show that W satisfies the differential equation
- <math>z(1+W)\frac{dW}{dz}=W\quad\mathrm{for\ }z\neq -1/e<math>
The Taylor series of W0 around 0 can be found using the Lagrange inversion theorem and is given by
- <math>
W_0 (x) = \sum_{n=1}^\infty \frac{(-n)^{n-1}}{n!}\ x^n = x - x^2 + \frac{3}{2}x^3 - \frac{8}{3}x^4 + \frac{125}{24}x^5 - \cdots <math>
The radius of convergence is 1/e, as may be seen by the ratio test. The function defined by this series can be extended to a holomorphic function defined on all complex numbers with a branch cut along the interval (−∞, −1/e]; this holomorphic function is defines the principal branch of the Lambert W function.
Many equations involving exponentials can be solved using the W function. The general strategy is to move all instances of the unknown to one side of the equation and make it look like x ex, at which point the W function provides the solution. For instance, to solve the equation 2t = 5t, we divide by 2t to get 1 = 5t e−ln(2)t, then divide by 5 and multiply by −ln(2) to get −ln(2)/5 = −ln(2)t e−ln(2)t. Now application of the W function yields −ln(2)t = W(−ln(2)/5), i.e. t = −W(−ln(2)/5) / ln(2).
Similar techniques show that
- <math>x^x=z<math>
has solution
- <math>x=\frac{\ln(z)}{W(\ln z)}<math>
or, equivalently,
- <math>x=\exp\left(W(\ln(z)\right).<math>
The function W(x), and many expressions involving W(x), can be integrated using the substitution w = W(x), i.e. x = w ew:
- <math>
\int W(x)\, dx = x \left( W(x) - 1 + \frac{1}{W(x)} \right) + C <math>
Special values
- <math>W\left(-\frac{\pi}{2}\right) = \frac{i\pi}{2}<math>
- <math>W\left(-{1\over e}\right) = -1<math>
- <math>W\left(-\frac{\ln 2}{2}\right)= -\ln 2<math>
- <math>W(0) = 0\,<math>
- <math>W(e) = 1\,<math>
- <math>W(1) = \Omega\,<math> (the Omega constant)
Evaluation algorithm
The W function may be evaluated using the recurrence relation
- <math>
w_{j+1}=w_j-\frac{w_j e^{w_j}-z}{e^{w_j}(w_j+1)-\frac{(w_j+2)(w_je^{w_j}-z)} {2w_j+2}} <math>
given in Corless et. al. to compute W. Together with the evaluation error estimate given in Chapeau-Belandeau and Monir, the following Python code implements this:
import math class Error(Exception): pass def lambertW(x, prec=1e-12): w = 0 for i in xrange(100): wTimesExpW = w*math.exp(w) wPlusOneTimesExpW = (w+1)*math.exp(w) if prec>abs((x-wTimesExpW)/wPlusOneTimesExpW): break w = w-(wTimesExpW-x)/( wPlusOneTimesExpW-(w+2)*(wTimesExpW-x)/(2*w+2)) else: raise Error, "W doesn't converge fast enough for %f"%x return w
This computes the principal branch for <math>x>1/e<math>. It could be improved by giving better initial estimates.
The following closed form approximation may be used by itself when less accuracy is needed, or to give an excellent initial estimate to the above code, which then may need only a few iterations:
double
desy_lambert_W(double x) {
double lx1;
if (x <= 500.0) {
lx1 = log(x + 1.0);
return 0.665 * (1 + 0.0195 * lx1) * lx1 + 0.04;
}
return log(x - 4.0) - (1.0 - 1.0/log(x)) * log(log(x));
}
(from http://www.desy.de/~t00fri/qcdins/texhtml/lambertw/)
References and external links
- Corless et.al. "On the Lambert W function" Adv. Computational Maths. 5, 329 - 359 (1996) (http://www.apmaths.uwo.ca/~djeffrey/Offprints/W-adv-cm.ps) (PostScript)
- Chapeau-Blondeau, F. and Monir, A: "Evaluation of the Lambert W Function and Application to Generation of Generalized Gaussian Noise With Exponent 1/2", IEEE Trans. Signal Processing, 50(9), 2002 (http://www.istia.univ-angers.fr/~chapeau/papers/lambertw.pdf)
- MathWorld - Lambert W-Function (http://mathworld.wolfram.com/LambertW-Function.html)
- Lambert function (http://functions.wolfram.com/ElementaryFunctions/ProductLog/) from Wolfram's function site.fr:Fonction W de Lambert