Tree structure
|
|
A tree structure is a way of representing the hierarchical nature of a structure in a graphical form. It is named a "tree structure" because the graph looks a bit like a tree, even though the tree is generally shown upside down compared with a real tree; that is to say with the root at the top and the leaves at the bottom.
In graph theory, a tree is a connected acyclic graph (or sometimes, a connected directed acyclic graph in which every vertex has indegree 0 or 1). An acyclic graph which is not necessarily connected is sometimes called a forest (because it is a set of trees).
Every finite tree structure has a member that has no superior. This member is called the "root" or root node. The converse is not true: infinite tree structures need not have a root node.
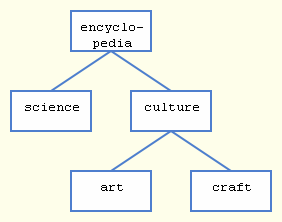
Illustration: A tree structure showing the possible hierarchical organization of an encyclopedia. This specific example happens to be a complete binary tree, which means all nodes have exactly zero or two child nodes.
The lines connecting elements are called "branches," the elements themselves are called "nodes." Nodes without children are called "end-nodes" or "leaves."
The names of relationships between nodes are modeled after family relations. In computer science, traditionally only names for male family members had been used. In linguistics, the names of female family members are used. It is said that this was an express countermovement to the traditional naming convention, started by the female students of linguist Noam Chomsky. However, nowadays, in computer science at least, the gender-neutral names "parent" and "child" have largely displaced the older "father" and "son" terminology.
The starting node is often called the "root."
- A node is a "parent" of another node if it is one step higher in the hierarchy and closer to the root node.
- "Sibling" ("brother" or "sister") nodes share the same parent node.
- A node that is connected to all lower-level nodes is called an "ancestor."
In the example, "encyclopedia" is the parent of "science" and "culture," its children. "Art" and "craft" are siblings, and children of "culture."
Tree structures are used to depict all kinds of taxonomic knowledge, such as family trees, the Evolutionary tree, the grammatical structure of a language (the famous example being S -> NP VP, meaning a sentence is a noun phrase and a verb phrase), the way web pages are logically ordered in a web site, et cetera.
Trees have a number of interesting properties:
- The root node, i.e., the base node, is an ancestor of all the other nodes.
- In a tree structure there is one and only one path from any point to any other point.
Tree structures are used extensively in computer science and telecommunications.
Examples of tree structures
- Internet: usenet hierarchy, Yahoo! subject index, Open Directory Project
- Information management: Dewey Decimal System
- Management: hierarchical organizational structures
- Computer Science: binary search tree
- Biology: evolutionary tree
- Business: pyramid selling scheme
- Project management: work breakdown structure
Representing trees
There are many ways of visually representing tree structures. Almost always, these boil down to variations, or combinations, of a few basic styles:
- Classical node-link diagrams, that connect nodes together with line segments:
encyclopedia
/ \
science culture
/ \
art craft
- Nested sets that use enclosure/containment to show parenthood (for an interesting variation on this, see Treemaps (http://www.cs.umd.edu/hcil/treemap-history/)):
+------encyclopedia------+
| +--culture--+ |
| science |art craft| |
| +-----------+ |
+------------------------+
- Layered "icicle" diagrams that use alignment/adjacency:
+-------------------+
| encyclopedia |
+---------+---------+
| science | culture |
+---------+---+-----+
|art|craft|
+---+-----+
- Diagrams that use indentation:
encyclopedia
science
culture
art
craft
Identification of some of these basic styles can be found in:
- Donald E. Knuth, The Art of Computer Programming, Volume I: Fundamental Algorithms, 1968, Addison-Wesley, pp. 309-310;
- Peter Eades, Tao Lin, and Xuemin Lin, Two Tree Drawing Conventions, International Journal of Computational Geometry and Applications, 1993, volume 3, number 2, pp. 133-153.
