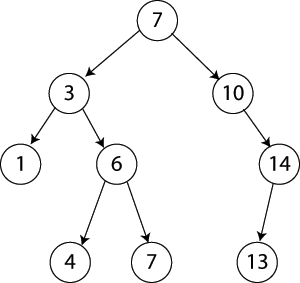
Binary search tree

In computer science, a binary search tree (BST) is a binary tree where every node has a value, every node's left subtree contains only values less than or equal to the node's value, and every node's right subtree contains only values that are greater than or equal. (Depending on the application of the binary search tree, equal values may not be allowed in either the left or right subtree). This requires that the values have a linear order. New nodes are added as leaves. Sort algorithms and search algorithms exist for binary search trees. The values of a binary search tree can be retrieved in ascending order using an in-order traversal.

Contents

1 Operations 1.1 Search 1.2 Insertion 1.3 Deletion 1.4 Traversal 1.5 Sort 2 Types of binary search trees 3 External links

Operations

Search

Searching a binary tree for a specific value is a recursive process that we can perform due to the ordering it imposes. We begin by examining the root. If the value equals the root, the value exists in the tree. If it is less than the root, then it must be in the left subtree, so we recursively search the left subtree in the same manner. Similarly, if it is greater than the root, then it must be in the right subtree, so we recursively search the right subtree in the same manner. If we reach an external node, then the item is not where it would be if it were present, so it does not lie in the tree at all. A comparison may be made with binary search, which operates in nearly the same way but using random access on an array instead of following links.

Here is the search algorithm in the Python programming language:

def search_binary_tree(treenode, value):
    if treenode is None: return None  # failure
    left, nodevalue, right = treenode
    if nodevalue > value:
        return search_binary_tree(left, value)
    elif value > nodevalue:
        return search_binary_tree(right, value)
    else:
        return nodevalue

This operation requires O(log n) time in the average case, but at worst-case is O(n), when the unbalanced tree resembles a linked list.

Insertion

Insertion begins with a search; we search for the value, but if we do not find it, we search the left or right subtrees as before. Eventually, we will reach an external node, and we add the value at that position. In other words, we examine the root and recursively insert the new node to the left subtree if the new value is less than or equal the root, or the right subtree if the new value is greater than the root.

Here is the insert algorithm in Python:

def binary_tree_insert(treenode, value):
    if treenode is None: return (None, value, None)
    left, nodevalue, right = treenode
    if nodevalue > value:
        return (binary_tree_insert(left, value), nodevalue, right)
    else:
        return (left, nodevalue, binary_tree_insert(right, value))

This operation requires O(log n) time in the average case, but at worst-case is O(n).

Deletion

There are several cases to consider:

• Deleting a leaf: Deleting a node with no children is easy, as we can simply remove it from the tree.
• Deleting a node with one child: Delete it and replace it with its child.
• Deleting a node with two children: Suppose the node to be deleted is called N. We replace the value of N with either its in-order successor (the left-most child of the right subtree) or the in-order predecessor (the right-most child of the left subtree).

Once we find either the in-order successor or predecessor, swap it with N, and then delete it. Since either of these nodes must have less than two children (otherwise it cannot be the in-order successor or predecessor), it can be deleted using the previous two cases.

In a good implementation, it is generally recommended to avoid consistently using one of these nodes, because this can unbalance the tree.

Here is Python code for deletion:

def binary_tree_delete(treenode, value):
    if treenode is None: return None # Value not found
    left, nodevalue, right = treenode
    if nodevalue == value:
        if   left  is None: 
            return right
        elif right is None: 
            return left
        else:
            maxvalue, newleft = find_remove_max(left)
            return (newleft, maxvalue, right)
    elif value < nodevalue:
        return (binary_tree_delete(left, value), nodevalue, right)
    else:
        return (left, nodevalue, binary_tree_delete(right, value))

def find_remove_max(treenode):
    left, nodevalue, right = treenode
    if right is None: return (nodevalue, left)
    else:
        (maxvalue, newright) = find_remove_max(right)
        return (maxvalue, (left, nodevalue, newright))

Although this operation does not always traverse the tree down to a leaf, this is always a possibility; thus in the worst case, it requires time proportional to the height of the tree. It does not require more even when the node has two children, since it still follows a single path and visits no node twice. Hence, deletion occurs in O(n) time.

Traversal

Once the binary search tree has been created, its elements can be retrieved in order by recursively traversing the left subtree, visiting the root, then recursively traversing the right subtree. The tree may also be traversed in pre order or post order traversals.

def traverse_binary_tree(treenode):
    if treenode is None: return
    left, nodevalue, right = treenode
    traverse_binary_tree(left)
    visit(nodevalue)
    traverse_binary_tree(right)

Traversal requires O(n) time, since it must visit every node.

Sort

A binary search tree can be used to implement a simple but inefficient sort algorithm. To do this, we insert all the values we wish to sort into a new binary search tree, then traverse it in order, building our result:

def build_binary_tree(values):
    tree = None
    for v in values:
        tree = binary_tree_insert(tree, v)
    return tree

def traverse_binary_tree(treenode):
    if treenode is None: return []
    else:
        left, value, right = treenode
        return (traverse_binary_tree(left) + [value] + traverse_binary_tree(right))

The worst-case time of build_binary_tree is O(n²) — if you feed it a sorted list of values, it chains them into a linked list with no left subtrees. For example, build_binary_tree([1, 2, 3, 4, 5]) yields the tree (None, 1, (None, 2, (None, 3, (None, 4, (None, 5, None))))). There are a variety of schemes for overcoming this flaw with simple binary trees; the most common is the self-balancing binary search tree. If this same procedure is done using such a tree, the overall worst-case time is the ideal O(nlog n).

Types of binary search trees

There are many types of binary search trees. AVL trees and red-black trees are both forms of self-balancing binary search trees. A splay tree is a binary search tree that automatically moves frequently accessed elements nearer to the root. In a treap ("tree heap"), each node also holds a priority and the parent node has higher priority than its children.

External links

• An introduction to binary trees from Stanford (http://cslibrary.stanford.edu/110/)
• Power Programming - Binary Tree (http://www.bitesizeinc.net/power.programming.binary.tree.html)
• Dictionary of Algorithms and Data Structures - Binary Search Tree (http://www.nist.gov/dads/HTML/binarySearchTree.html)da:Binært søgetræ

de:binärer Suchbaum he:עץ חיפוש pl:Drzewo poszukiwań binarnych uk:Бінарне дерево пошуку zh:二叉查找树