Finite state machine

A finite state machine (FSM) or finite automaton is a model of behaviour composed of states, transitions and actions. A state stores information about the past, i.e. it reflects the input changes from the system start to the present moment. A transition indicates a state change and is described by a condition that would need to be fulfilled to enable the transition. An action is a description of an activity that is to be performed at a given moment. There are several action types:

Entry action

execute the action when entering the state

Exit action

execute the action when exiting the state

Input action

execute the action dependant on present state and input conditions

Transition action

execute the action when performing a certain transition

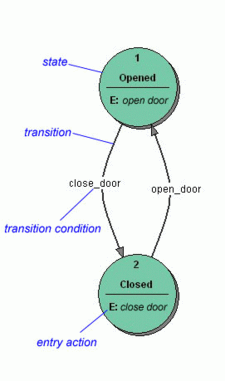
FSM can be represented using a state diagram (or state transition diagram) as in figure 1. Besides this, several state transition table types are used. The most common representation is shown below: the combination of current state (B) and condition (Y) shows the next state (C). The complete actions information can be added only using footnotes. An FSM definition including the full actions information is possible using state tables (see also VFSM).

State transition table

Current State/ Condition	State A	State B	State C
Condition X	...	...	...
Condition Y	...	State C	...
Condition Z	...	...	...

FSM was originally defined in the automata theory and later taken over in the theory of computation.

Finite state machines are very widely used in modelling of application behaviour, design of hardware digital systems, software engineering, study of computation and languages.

Contents

1 Classification 1.1 Acceptors and recognizers 1.2 Transducers 2 FSM logic 3 Mathematical model 4 Optimization 5 Implementation 5.1 Hardware applications 5.2 Software applications 6 Tools 7 References 8 See also 9 External links

Classification

There are two groups distinguished: Acceptors/Recognizers and Transducers.

Acceptors and recognizers

They accept/recognize their input and use states to signal the result to the outside world. As a rule the input are symbols (characters). Actions are not used. The example in figure 2 shows a finite state machine which accepts the word "nice":

Transducers

Transducers generate output based on a given input and/or a state using actions. They are used for control applications. Here two types are distinguished:

Moore machine

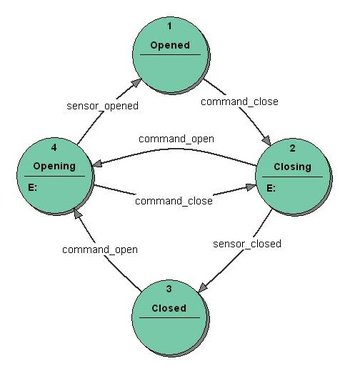
The FSM uses only entry actions, i.e. output depends only on the state. The advantage of the Moore model is a simplification of the behaviour. The example in figure 3 shows a Moore FSM of an elevator door. The state machine recognizes two commands: "command_open" and "command_close" which trigger state changes. The entry action (E:) in state "Opening" starts a motor opening the door, the entry action in state "Closing" starts a motor in the other direction closing the door. States "Opened" and "Closed" don't perform any actions. They signal to the outside world (e.g. to other state machines) the situation: "door is open" or "door is closed".

Mealy machine

The FSM uses only input actions, i.e. output depends on input and state. The use of a Mealy FSM leads often to a reduction of the number of states. The example in figure 4 shows a Mealy FSM implementing the same behaviour as in the Moore example (the behaviour depends on the implemented FSM execution model and will work e.g. for virtual FSM but not for event driven FSM). There are two input actions (I:): "start motor to close the door if command_close arrives" and "start motor in the other direction to open the door if command_open arrives".

In practice mixed models are often used.

More details about the differences and usage of Moore and Mealy models, including an executable example, can be found in the external technical note "Moore or Mealy model?" (http://www.stateworks.com/active/content/en/technology/technical_notes.php#tn10)

A further distinction is between deterministic (DFA) and non-deterministic (NDFA, GNFA) automata. In deterministic automata, for each state there is exactly one transition for each possible input. In non-deterministic automata, there can be none or more than one transition from a given state for a given possible input.

The FSM with only one state is called a combinatorial FSM and uses only input actions. This concept is useful in cases where a number of FSM are required to work together, and where it is convenient to consider a purely combinatorial part as a form of FSM to suit the design tools.

FSM logic

The next state and output of a FSM is a function of the input and of the current state. The FSM logic is shown in Figure 5

Mathematical model

Depending on the type there are several definitions. An acceptor finite state machine is a quintuple <Σ, S, s0, δ, F>, where:

• Σ is the input alphabet (a finite non empty set of symbols),
• S is a finite non empty set of states,
• s0 is an initial state, an element of S,
• δ is the state transition function: δ = S x Σ → S,
• F is the set of final states, a (possibly empty) subset of S.

A transducer finite state machine is a sextuple <Σ, Γ, S, s0, δ, ω>, where:

• Σ is the input alphabet (a finite non empty set of symbols),
• Γ is the output alphabet (a finite non empty set of symbols),
• S is a finite non empty set of states,
• s0 is an initial state, an element of S,
• δ is the state transition function: δ: S x Σ → S,
• ω is the output function.

If the output function is a function of a state and input alphabet (ω: S x Σ → Γ) that definition corresponds to the Mealy model. If the output function depends only on a state (ω: S → Γ) that definition corresponds to the Moore model.

Optimization

Optimizing an FSM means finding the machine with the minimum number of states that performs the same function. This problem can be solved using a coloring algorithm.

Implementation

Hardware applications

In a digital circuit, a FSM may be built using a programmable logic device, a programmable logic controller, logic gates and flip flops or relays. More specifically, a hardware implementation requires a register to store state variables, a block of combinational logic which determines the state transition, and a second block of combinational logic that determines the output of a FSM.

Software applications

Following concepts are commonly used to build software applications with finite state machines:

• event driven FSM
• virtual FSM (VFSM)

Tools

AT&T FSM Library™ [1] (http://www.research.att.com/projects/mohri/fsm/) AutoFSM [2] (http://autogen.sourceforge.net/autofsm.html) Bandera [3] (http://bandera.projects.cis.ksu.edu/) CAZE - FSM-based .NET authorization library [4] (http://www.lamarvin.com/caze_default.asp) Covered [5] (http://covered.sourceforge.net/) Concurrent Hierarchical State Machine [6] (http://homepage.mac.com/pauljlucas/software/chsm/) Dynamic Attachment Finite State Machine (DAFSM) [7] (http://dmabco.sourceforge.net/) Exorciser [8] (http://www.educeth.ch/compscience/exorciser/) Finite State Kernel Creator [9] (http://fskc.sourceforge.net/) Finite State Machine Editor [10] (http://fsme.sourceforge.net/) Finite State Machine Explorer [11] (http://www.belgarath.org/java/fsme.html)

FSMGenerator [12] (http://fsmgenerator.sourceforge.net/) FSA Utilities [13] (http://odur.let.rug.nl/~vannoord/Fsa/) JFLAP [14] (http://www.cs.duke.edu/~rodger/tools/jflap/) jrexx-Lab [15] (http://www.karneim.com/jrexx/) JSpasm [16] (http://jspasm.sourceforge.net/) Kara [17] (http://www.swisseduc.ch/informatik/karatojava/) Nunni FSM Generator [18] (http://nunnifsmgen.nunnisoft.ch/en/) Petrify [19] (http://www.lsi.upc.edu/~jordicf/petrify/) Qfsm [20] (http://qfsm.sourceforge.net/) Quantum-Leaps [21] (http://www.quantum-leaps.com/) Ragel [22] (http://www.elude.ca/ragel/)

RWTH FSA Toolkit [23] (http://www-i6.informatik.rwth-aachen.de/web/Software/index.html) Statestep [24] (http://statestep.com/) StateWORKS [25] (http://www.stateworks.com/) State Machine Compiler [26] (http://smc.sourceforge.net/) UniMod [27] (http://unimod.sourceforge.net/) WhatOS [28] (http://www.sticlete.com/whatos/) Xerox Finite-State Software Tools [29] (http://www.xrce.xerox.com/competencies/content-analysis/fssoft/home.en.html)

References

• Timothy Kam, Synthesis of Finite State Machines: Functional Optimization. Kluwer Academic Publishers, Boston 1997, ISBN 0-7923-9842-4
• Tiziano Villa, Synthesis of Finite State Machines: Logic Optimization. Kluwer Academic Publishers, Boston 1997, ISBN 0-7923-9892-0
• Carroll, J., Long, D. , Theory of Finite Automata with an Introduction to Formal Languages. Prentice Hall. Englewood Cliffs, 1989.
• Hopcroft, J.E., Ullman, J.D., Introduction to Automata Theory, Languages and Computation. Adison -Wesley, 1979.
• Kohavi, Z., Switching and Finite Automata Theory. McGraw-Hill, 1978.
• Gill, A., Introduction to the Theory of Finite-state Machines. McGraw-Hill, 1962.
• Cassandras, C., Lafortune, S., "Introduction to Discrete Event Systems". Kluwer, 1999, ISBN 0-7923-8609-4

See also

• Pushdown automaton
• Turing machine
• Petri net
• Simulation
• Marvin Minsky
• Automata analyzer
• Coverage analysis
• Transition system
• Protocol development
• Automaton
• Abstract state machine
• Automata theory
• Sparse matrix

External links

• Description from the Free On-Line Dictionary of Computing (http://foldoc.doc.ic.ac.uk/foldoc/foldoc.cgi?query=finite+state+machine)
• Citations from CiteSeer (http://citeseer.ist.psu.edu/cs?q=finite+state+machine)
• NIST Dictionary of Algorithms and Data Structures entry (http://www.nist.gov/dads/HTML/finiteStateMachine.html)
• Hierarchical State Machines (http://www.eventhelix.com/RealtimeMantra/HierarchicalStateMachine.htm)bg:Краен автомат

cs:KoneÄ�ný automat de:Endlicher Automat es:Autómata finito fi:Äärellinen automaatti fr:Machine à états finis he:אוטומט סופי ru:Конечный автомат zh:有限状态自动机