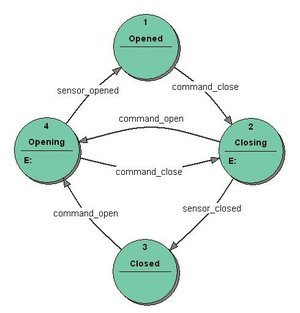
Moore machine
|
|
In the theory of computation, a Moore machine is a finite state automaton where the outputs are determined by the current state alone (and not on the input). The state diagram for a Moore machine will include an output signal for each state. Compare with a Mealy machine, which maps transitions in the machine to outputs.
The name Moore machine comes from that of their promoter: E. F. Moore, a state machine pioneer, who wrote Gedanken-experiments on Sequential Machines, pp 129 – 153, Automata Studies, Annals of Mathematical Studies, no. 34, Princeton University Press, Princeton, N. J., 1956
Most electronics are designed as clocked sequential systems. Clocked sequential systems are a restricted form of Moore machine where the state changes only when the global clock signal changes. Typically the current state is stored in flip-flops, and global clock signal is connected to the "clock" input of the flip-flops. Clocked sequential systems are one way to solve metastability problems.
Formal definition
A Moore machine can be defined as a 7-tuple
{ Q, Σ, Δ, δ, λ, <math>q_0<math>, F } consisting of
- a finite set of states ( Q )
- a finite set called the input alphabet ( Σ )
- a finite set called the output alphabet ( Δ )
- a transition function (δ : Q x Σ → Q ) mapping a state and an input to the next state
- an output function ( λ : Q → Δ ) mapping each state to the output alphabet.
- a start state <math>( q_0 )<math>
- a set of finish states F
The number of states in a Moore machine will be greater than or equal to the number of states in the corresponding Mealy machine.de:Moore-Automat zh:Moore有限状态机