Covariance and contravariance
|
|
This page does not deal with the statistical concept covariance of random variables, nor with the computer science concepts of parameter covariance and contravariance
In mathematics and theoretical physics, covariance and contravariance are concepts used in many areas, generalising in a sense invariance, i.e. the property of being unchanged under some transformation. In mathematical terms they occur in a foundational way in linear algebra and multilinear algebra, differential geometry and other branches of geometry, category theory and algebraic topology. In physics they are important to the treatment of vectors and other quantities, such as tensors, that have physical meaning but are not scalars. Both special relativity (Lorentz covariance) and general relativity (general covariance) use covariance as basic.
In very general terms, duality interchanges covariance and contravariance, which is why these concepts occur together. For purposes of practical computation using matrices, the transpose relates two aspects (for example two sets of simultaneous equations). The case of a square matrix for which the transpose is also the inverse matrix, that is, an orthogonal matrix, is one in which covariance and contravariance can typically be treated on the same footing. This is of basic importance in the practical application of tensors.
A major potential cause of confusion is that this duality of covariance/contravariance intervenes every time discussion of a vector or tensor quantity is represented by its components. This causes discussion in the mathematics and physics literature often apparently to be using opposite conventions. It is not the convention that differs, but whether an intrinsic or component-wise description is the primary way of thinking of quantities. As the names suggest, covariant quantities are thought of as moving or transforming forwards, while contravariant quantities transform backwards. Which is which does depend on whether one is using any fixed background: in fact that switches the point of view.
| Contents |
Informal usage
In common physics usage, the adjective covariant may sometimes be used informally as a synonym for invariant (or equivariant, in mathematicians' terms). For example, the Schrödinger equation does not keep its written form under the coordinate transformations of special relativity; thus one might say that the Schrödinger equation is not covariant. By contrast, the Klein-Gordon equation and the Dirac equation take the same form in any coordinate frame of special relativity: thus, one might say that these equations are covariant. More properly, one should really say that the Klein-Gordon and Dirac equations are invariant, and that the Schrödinger equation is not, but this is not the dominant usage. Note also that neither the Klein-Gordon nor the Dirac equations are invariant under the transformations of general relativity (nor are they in any sense covariant either), and thus proper use should indicate what the invariance is in respect to.
Similar informal usage is sometimes seen with respect to quantities like mass and time in general relativity: mass is techically a component of the four-momentum or the energy-momentum tensor, but one might occasionally see language refering to the covariant mass, meaning the length of the momentum four-vector.
Example: covariant basis vectors in Euclidean R3
If e1, e2, e3 are contravariant basis vectors of R3 (not necessarily orthogonal nor of unit norm) then the covariant basis vectors of their reciprocal system are:
- <math> \mathbf{e}_1 = \frac{\mathbf{e}^2 \times \mathbf{e}^3}{\mathbf{e}^1 \cdot \mathbf{e}^2 \times \mathbf{e}^3} ; \qquad \mathbf{e}_2 = \frac{\mathbf{e}^3 \times \mathbf{e}^1}{\mathbf{e}^1 \cdot \mathbf{e}^2 \times \mathbf{e}^3}; \qquad \mathbf{e}_3 = \frac{\mathbf{e}^1 \times \mathbf{e}^2}{\mathbf{e}^1 \cdot \mathbf{e}^2 \times \mathbf{e}^3}
<math>
Then the contravariant coordinates of any vector v can be obtained by the dot product of v with the contravariant basis vectors:
- <math> q^1 = \mathbf{v \cdot e^1}; \qquad q^2 = \mathbf{v \cdot e^2}; \qquad q^3 = \mathbf{v \cdot e^3} <math>
Likewise, the covariant components of v can be obtained from the dot product of v with covariant basis vectors, viz.
- <math> q_1 = \mathbf{v \cdot e_1}; \qquad q_2 = \mathbf{v \cdot e_2}; \qquad q_3 = \mathbf{v \cdot e_3} <math>
Then v can be expressed in two (reciprocal) ways, viz.
- <math> \mathbf{v} = q_i \mathbf{e}^i = q_1 \mathbf{e}^1 + q_2 \mathbf{e}^2 + q_3 \mathbf{e}^3 <math>
- <math> \mathbf{v} = q^i \mathbf{e}_i = q^1 \mathbf{e}_1 + q^2 \mathbf{e}_2 + q^3 \mathbf{e}_3 <math>.
The indices of covariant coordinates, vectors, and tensors are subscripts (but see above, note on notation convention). If the contravariant basis vectors are orthonormal then they are equivalent to the covariant basis vectors, so there is no need to distinguish between the covariant and contravariant coordinates, and all indices are subscripts.
What 'contravariant' means
Contravariant is a mathematical term with a precise definition in tensor analysis. It specifies precisely the method (direction of projection) used to derive the components by projecting the magnitude of the tensor quantity onto the coordinate system being used as the basis of the tensor.
Another method is used to derive covariant tensor components. When performing tensor transformations it is critical that the method used to map to the coordinate systems in use be tracked so that operations may be applied correctly for accurate, meaningful results.
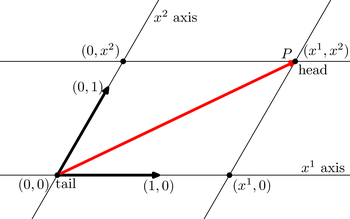
In two dimensions, for an oblique rectilinear coordinate system, contravariant coordinates of a directed line segment (in two dimensions this is termed a vector) can be established by placing the origin of the coordinate axis at the tail of the vector. Parallel lines are placed through the head of the vector. The intersection of the line parallel to the x1 axis with the x2 axis provides the x2 coordinate. Similarly, the intersection of the line parallel to the x2 axis with the x1 axis provides the x1 coordinate.
By definition, the oblique, rectilinear, contravariant coordinates of the point P above are summarized as: xi = (x1, x2)
Notice the superscript; this is a standard nomenclature convention for contravariant tensor components and should not be confused with the subscript, which is used to designate covariant tensor components.
Is there a fundamental difference in the way contravariant and covariant components can be used, or could one simply interchange them everywhere? The answer is that in curved spaces, or in curved coordinate systems in flat space (e.g. cylindrical coordinates in Euclidean space), the quantity dxi is a perfect differential that can be immediately integrated to yield xi, whilst the covariant components of the same differential, dxi are not in general perfect differentials; the integrated change depends on the path. In the example of cylindrical coordinates, for example, the radial and z components are the same in covariant and contravariant form, but the covariant component of the differential of angle round the z axis is r2dθ and its integral depends on the path.
Using the definition above, the contravariant components of a position vector vi, where i = {1, 2}, can be defined as the differences between coordinates (or position vectors) of the head and tail, on the same coordinate axis. Stated in another way, the vector components are the projection onto an axis from the direction parallel to the other axis.
So, since we have placed our origin at the tail of the vector,
- vi = ( (x1 − 0), (x2 − 0 ) )
- vi = (x1, x2)
This result is generalized into n-dimensions. Contravariance is a fundamental concept or property within tensor theory and applies to tensors of all ranks over all manifolds. Since whether tensor components are contravariant or covariant, how they are mixed, and the order of operations all impact the results it is imperative to track for correct application of methods.
In more modern terms, the transformation properties of the covariant indices of a tensor are given by a pullback; by contrast, the transformation of the contravariant indices is given by a pushforward.
Usage in tensor analysis
In tensor analysis, a covariant vector varies more or less reciprocally to a corresponding contravariant vector. Expressions for lengths, areas and volumes of objects in the vector space can then be given in terms of tensors with covariant and contravariant indices. Under simple expansions and contractions of the coordinates, the reciprocity is exact; under affine transformations the components of a vector intermingle on going between covariant and contravariant expression.
On a manifold, a tensor field will typically have multiple indices, of two sorts. By a widely followed convention (including Wikipedia), covariant indices are written as lower indices, whereas contravariant indices are upper indices. When the manifold is equipped with a metric, covariant and contravariant indices become very closely related to one-another. Contravariant indices can be turned into covariant indices by contracting with the metric tensor. Contravariant indices can be gotten by contracting with the (matrix) inverse of the metric tensor. Note that in general, no such relation exists in spaces not endowed with a metric tensor. Furthermore, from a more abstract standpoint, a tensor is simply "there" and its components of either kind are only calculational artifacts whose values depend on the chosen coordinates.
The explanation in geometric terms is that a general tensor wil have contravariant indices as well as covariant indices, because it has parts that live in the tangent bundle as well as the cotangent bundle.
Algebra and geometry
In category theory, see covariant functor (which is the default meaning for functor) and contravariant functor. The dual space is a standard example of a contravariant construction and tensor. Some constructions of multilinear algebra are of 'mixed' variance, which prevents them from being functors as such. The distinction between homology theory and cohomology theory in topology is that homology is covariant, while cohomology is contravariant (it was suggested in a book, Hilton & Wylie, that contrahomology was therefore a better term for cohomology, but this did not catch on). Homology theory is covariant because (as is very clear in singular homology) its basic construction is to take a topological space X and map things into it (in that case, simplices). For a continuous mapping from X to another space Y, simply map on by composing functions. Cohomology goes the 'other way'; this is adapted to studying mappings out of X, for example the sections of a vector bundle.
In geometry, the same map in/map out distinction is helpful in assessing the variance of constructions. A tangent vector to a smooth manifold M is, to begin with, a curve mapping smoothly into M and passing through a given point P. It is therefore covariant, with respect to smooth mappings of M. A contravariant vector, or 1-form, is in the same way constructed from a smooth mapping from M to the real line, near P. It is in the cotangent bundle, built up from the dual spaces of the tangent spaces. Its components with respect to a local basis of one-forms dxi will be covariant; but one-forms and differential forms in general are contravariant, in the sense that they pull back under smooth mappings. This is crucial to how they are applied; for example a differential form can be restricted to any submanifold, while this does not make the same sense for a field of tangent vectors.
Covariant and contravariant indices transform in different ways under coordinate transformations. By considering a coordinate transformation on a manifold as a map from the manifold to itself, the transformation of covariant indices of a tensor are given by a pullback, and the transformation properties of the contravariant indices is given by a pushforward.
See also: covariant transformation