Bohr model
|
|
| Contents [hide] |
History
In the early part of the 20th century, experiments by Ernest Rutherford and others had established that atoms consisted of negatively charged electrons orbiting a small, dense, positively charged nucleus.
The simplest possible atom is hydrogen, which consists of one proton and one electron bound together by the coulomb force. This is in contrast to the Earth-Sun system, which is held together by the gravitational force.
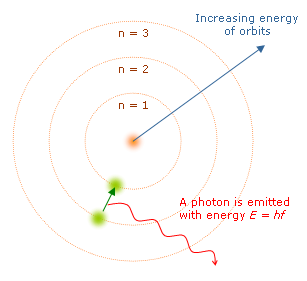
Another difference is that electron (in this model) can only be at certain, discrete, distances from the proton it's bound to. If it could be at any distance, it would lose energy (by synchrotron radiation) and eventually spiral into the proton - destroying the atom in the process. Additional support for the Bohr Model came from atomic spectra, which showed that orbiting electrons could only emit light at certain frequencies and energies.
Thus in 1913, Niels Bohr proposed that:
- (1) The orbiting electrons existed in orbits that had discrete quantized energies. That is, not every orbit is possible but only certain specific ones.
- (2) The laws of classical mechanics do not apply when electrons make the jump from one allowed orbit to another.
- (3) When an electron makes a jump from one orbit to another the energy difference is carried off (or supplied) by a single quantum of light (called a photon) which has an energy equal to the energy difference between the two orbitals.
- (4) The allowed orbits depend on quantized (discrete) values of orbital angular momentum, L according to the equation
- <math> \mathbf{L} = n \cdot \hbar = n \cdot {h \over 2\pi} <math>
- Where n = 1,2,3,… and is called the angular momentum quantum number.
Assumption (4) states that the lowest value of n is 1. This corresponds to a smallest possible radius of 0.0529 nm. This is known as the Bohr radius. Once an electron is in this lowest orbit, it can get no closer to the proton.
For a more accurate description of an atom see quantum mechanics. The full quantum mechanical treatment of the atom is much more accurate - but it is mathematically much more complex, and often the much simpler Bohr model can produce usable results with much less hassle. The thing to remember is that like other models, it is only an aid to understanding. Atoms are not really little solar systems. Bohr's genius, though, was to begin a breakaway from this view that continues to this day.
Derivation of the Electron Energy Levels of Hydrogen
The Bohr model is actually only accurate for one-electron systems such as the hydrogen atom or singly-ionized helium. Here we use it to derive the energy levels of hydrogen.
We begin with three simple assumptions:
- 1) De Broglie hypothesis: all particles are wavelike, and an electron's wavelength <math>\lambda<math>, is related to its velocity v by:
- <math>\lambda = \frac{h}{m_e v}<math>
- where h is Planck's Constant, and <math>m_e<math> is the mass of the electron. De Broglie's hypothesis wasn't proposed until 10 years after the Bohr model, but using it is allows us to make the following intuitive statement.
- 2) The circumference of the electron's orbit must be an integer multiple of its wavelength:
- <math>2 \pi r = n \lambda \,<math>
- where r is the radius of the electron's orbit, and n is a positive integer.
- 3) The electron is held in orbit by the coulomb force. That is, the coulomb force is equal to the centripetal force:
- <math>\frac{ke^2}{r^2} = \frac{m_e v^2}{r} \,<math>
- where <math>k = 1 / {4 \pi \epsilon _0}<math>, and e is the charge of the electron.
These are three equations with three unknowns: <math>\lambda<math>, r, v. Putting these three together, and knowing that the total energy of the electron is
<math>E \,<math> <math>=E_{kinetic} + E_{potential} \,<math> <math>= \frac{1}{2}m_e v^2 - \frac{k e^2}{r} = -\frac{1}{2}m_e v^2<math>
we find an equation that gives us the different energy levels of Hydrogen:
<math>E _n \,<math> <math>= -2 \pi^2 k^2 \left( \frac{m_e e^4}{h^2} \right) \frac{1}{n^2} \,<math> <math>= \frac{-m_e e^4}{8 h^2 \epsilon_{0}^2} \frac{1}{n^2} \,<math> <math>= \frac{-13.6 eV}{n^2} \,<math>
Thus, the 1st (and lowest) energy level of hydrogen (n = 1) is -13.6 eV. The next energy level (n = 2) is -3.4 eV. The third (n = 3) is -1.51 eV, and so on.
Note that energies less than zero mean that the electron is in a bound state.
Transitions between energy levels (Rydberg Formula)
When the electron moves from one energy level to another, a photon is given off. Using the derived formula for the different 'energy' levels of Hydrogen we can now determine the 'wavelengths' of light that a Hydrogen atom can give off.
First, the energy of photons that a Hydrogen atom can give off are given by the difference of two Hydrogen energy levels:
- <math>E=E_i-E_f=\frac{m_e e^4}{8 h^2 \epsilon_{0}^2} \left( \frac{1}{n_{f}^2} - \frac{1}{n_{i}^2} \right) \,<math>
- where <math>n_f<math> means the final energy level, and <math>n_i<math> means the initial energy level. (We are assuming the final energy level is less than the initial energy level.)
And since the energy of a photon is
- <math>E=\frac{hc}{\lambda} \,<math>
The wavelength of the photon given off is
- <math>\frac{1}{\lambda}=\frac{m_e e^4}{8 c h^3 \epsilon_{0}^2} \left( \frac{1}{n_{f}^2} - \frac{1}{n_{i}^2} \right) \,<math>
- also known as the Rydberg formula.
This formula was known by scientists who did spectroscopy in the nineteenth century, but they had no theoretical justification for the formula until Bohr derived it this way.
Shortcomings of the Bohr model
It fails to explain:
- the spectra of larger atoms: it could at best approximately predict what atoms with one outer electron would do for spectral emissions
- the relative intensities of spectral lines
- the existence of hyperfine spectral lines
- the Zeeman effect - changes in spectral lines due to external magnetic fields
See also
- Franck-Hertz experiment
- Hydrogen atom
- Niels Bohr
- Lyman series
- quantum mechanics
- Rydberg formula
- Schrödinger equationda:Atommodel (Bohr)
de:Bohrsches Atommodell es:Modelo atómico de Bohr fr:Modèle de Bohr it:Modello atomico di Bohr lv:Bora atoma struktūras modelis nl:Atoommodel van Bohr fi:Bohrin malli