Vertex cover problem
|
|
In computer science, the vertex cover problem or node cover problem is an NP-complete problem in complexity theory, and was one of Karp's 21 NP-complete problems.
A vertex cover of an undirected graph <math>G = (V, E)<math> is a subset <math>V'<math> of the vertices of the graph which contains at least one of the two endpoints of each edge:
- <math>V' \subseteq V: \forall \{a, b\} \in E : a \in V' \or b \in V'<math>.
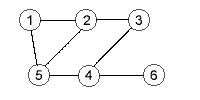
In the graph at the right, {1,3,5,6} is an example of a vertex cover.
The vertex cover problem is the optimization problem of finding a vertex cover of minimum size in a graph. The problem can also be stated as a decision problem:
- INSTANCE: A graph <math>G<math> and a positive integer <math>k<math>.
- QUESTION: Is there a vertex cover of size <math>k<math> or less for <math>G<math>?
Vertex cover is NP-complete, which means it is unlikely that there is an efficient algorithm to solve it. NP-completeness can be proven by reduction from 3-satisfiability or, as Karp did, by reduction from the clique problem. As shown by Garey and Johnson in 1974, vertex cover remains NP-complete even in cubic graphs and even in planar graphs of degree at most 6.
Vertex cover is closely related to Independent Set problem by this theorem: a graph with <math>n<math> vertices has a vertex cover of size <math>k<math> if and only if the graph has an independent set of size <math>n-k<math>.
One can find a factor-2 approximation by repeatedly taking both endpoints of an edge into the vertex cover, removing them from the graph. No better constant-factor approximation is known; the problem is APX-complete, i.e., it cannot be approximated arbitrarily well.
A brute force algorithm to find a vertex cover in a graph is to choose some vertex and recursively branch into two cases: either take this vertex into the vertex cover, or all its neighbors. This algorithm is exponential in <math>k<math>, but not in the size of the graph, i.e., vertex cover is fixed-parameter tractable with respect to <math>k<math>.
See also
Further reading
- Michael R. Garey and David S. Johnson. Computers and Intractability: A Guide to the Theory of NP-Completeness. W. H. Freeman & Co., New York, 1979.
- Preeti Patil & Sangita Patil. (Lecturer in Vartak Polytechnic) A Guide to the Theory of NP-Completeness. BPB & Co., Mumbai, 2004.
- M. R. Garey, D. S. Johnson, and L. Stockmeyer. Some simplified NP-complete problems (http://portal.acm.org/citation.cfm?id=803884). Proceedings of the sixth annual ACM symposium on Theory of computing, p.47-63. 1974.de:Knotenüberdeckung