NP-complete
|
|
In complexity theory, the NP-complete problems are the most difficult problems in NP, in the sense that they are the ones most likely not to be in P. The reason is that if you could find a way to solve an NP-complete problem quickly, then you could use that algorithm to solve all NP problems quickly. The complexity class consisting of all NP-complete problems is sometimes referred to as NP-C. (A more formal definition is given below. See also Complexity classes P and NP).
One example of an NP-complete problem is the subset sum problem which is: given a finite set of integers, determine whether any non-empty subset of them sums to zero. A supposed answer is very easy to verify for correctness, but no one knows a significantly faster way to solve the problem than to try every single possible subset, which is very slow.
| Contents |
Formal definition of NP-completeness
A decision problem C is NP-complete if
- it is in NP and
- every other problem in NP is reducible to it.
"Reducible" here means that for every problem L, there is a polynomial-time many-one reduction, a deterministic algorithm which transforms instances l ∈ L into instances c ∈ C, such that the answer to c is YES if and only if the answer to l is YES. To prove that a NP problem A is in fact a NP-complete problem we must show that an already known NP-complete problem reduces to A.
A consequence of this definition is that if we had a polynomial time algorithm for C, we could solve all problems in NP in polynomial time.
This definition was given by Stephen Cook in 1971 (although the term "NP-complete" did not appear in his paper). At first it seems rather surprising that NP-complete problems should even exist, but in a celebrated theorem Cook proved that the Boolean satisfiability problem is NP-complete. In 1972 Richard Karp proved that several other problems were also NP-complete (see Karp's 21 NP-complete problems); thus there is a class of NP-complete problems (besides the Boolean satisfiability problem). Since Cook's original results, thousands of other problems have been shown to be NP-complete by reductions from other problems previously shown to be NP-complete; many of these problems are collected in Garey and Johnson's 1979 book Computers and Intractability: A Guide to NP-Completeness.
A problem satisfying condition 2 but not necessarily condition 1 is said to be NP-hard. Informally, an NP-hard problem is "at least as hard as" any NP-complete problem, and perhaps harder. For example, choosing the perfect move in certain board games on an arbitrarily large board is NP-hard or even strictly harder than the NP-complete problems.
Example problems
An interesting example is the graph isomorphism problem, the graph theory problem of determining whether a graph isomorphism exists between two graphs. Two graphs are isomorphic if one can be transformed into the other simply by renaming vertices. Consider these two problems:
Graph Isomorphism: Is graph G1 isomorphic to graph G2?
Subgraph Isomorphism: Is graph G1 isomorphic to a subgraph of graph G2?
The Subgraph Isomorphism problem is NP-complete. The Graph Isomorphism problem is suspected to be neither in P nor NP-complete, though it is obviously in NP. This is an example of a problem that is thought to be hard, but isn't thought to be NP-complete.
The easiest way to prove that some new problem is NP-complete is first to prove that it is in NP, and then to reduce some known NP-complete problem to it. Therefore, it is useful to know a variety of NP-complete problems. Below are a few of them. For more examples of NP-complete problems, see List of NP-complete problems.
- Boolean satisfiability problem (SAT)
- Fifteen puzzle
- Knapsack problem
- Hamiltonian cycle problem
- Traveling salesman problem
- Subgraph isomorphism problem
- Subset sum problem
- Clique problem
- Vertex cover problem
- Independent Set problem
- Graph coloring problem
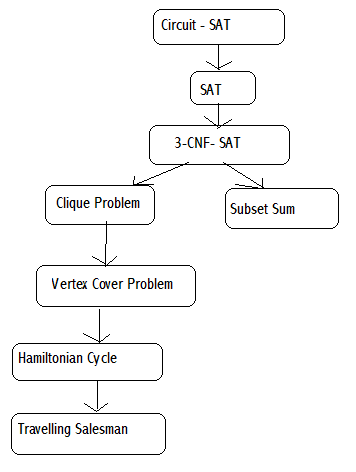
Here is a diagram of some of the NP-Complete problems and the reductions typically used to prove their NP-completeness. In this diagram, an arrow from one problem to another indicates the direction of the reduction. Note that this diagram is misleading as a description of the mathematical relationship between these problems, as there exists a polynomial-time reduction between any two NP-complete problems; but it indicates where demonstrating this polynomial-time reduction has been easiest.
There is often only a small difference between a problem in P and an NP-complete problem. For example, the 3SAT problem, a restriction of the boolean satisfiability problem, remains NP-complete, whereas the slightly more restricted 2SAT problem is in P, and the slightly more general MAX 2SAT problem is again NP-complete. Determining whether a graph can be colored with 2 colors is in P, but with 3 colors is NP-complete, even when restricted to planar graphs. Determining if a graph is a cycle or is bipartite is very easy (in L), but finding a maximum bipartite or a maximum cycle subgraph is NP-complete. A solution of the knapsack problem within any fixed percentage of the optimal solution can be computed in polynomial time, but finding the optimal solution is NP-complete.
Imperfect solutions
At present, all known algorithms for NP-complete problems require time that is superpolynomial in the input size. It is unknown whether there are any faster algorithms. Therefore, to solve an NP-complete problem for any nontrivial problem size, generally one of the following approaches is used:
- Approximation: An algorithm that quickly finds a suboptimal solution that is within a certain (known) range of the optimal one.
- Probabilistic: An algorithm that provably yields good average runtime behavior for a given distribution of the problem instances—ideally, one that assigns low probability to "hard" inputs.
- Special cases: An algorithm that is provably fast if the problem instances belong to a certain special case. Fixed-parameter algorithms can be seen as an implementation of this approach.
- Heuristic: An algorithm that works "reasonably well" on many cases, but for which there is no proof that it is both always fast and always produces a good result (a rule of thumb, intuition).
One example of a heuristic algorithm is a suboptimal O(n log n) greedy algorithm used for graph coloring during the register allocation phase of some compilers, a technique called graph-coloring global register allocation. Each vertex is a variable, edges are drawn between variables which are being used at the same time, and colors indicate the register assigned to each variable. Because most RISC machines have a fairly large number of general-purpose registers, even a heuristic approach is effective for this application.
Alternative approaches
In the definition of NP-complete given above, the term "reduction" was used in the technical meaning of polynomial-time many-one reduction.
Another type of reduction is polynomial-time Turing reduction. A problem X is polynomial-time Turing-reducible to a problem Y if, given a subroutine that solves Y in polynomial time, you could write a program that calls this subroutine and solves X in polynomial time. This contrasts with many-one reducibility, which has the restriction that the program can only call the subroutine once, and the return value of the subroutine must be the return value of the program.
If one defines the analogue to NP-complete with Turing reductions instead of many-one reductions, the resulting set of problems won't be smaller than NP-complete; it is an open question whether it will be any larger. If the two concepts were the same, then it would follow that NP = Co-NP. This holds because by their definition the classes of NP-complete and co-NP-complete problems under Turing reductions are the same and because these classes are both supersets of the same classes defined with many-one reductions. So if both definitions of NP-completeness are equal then there is a co-NP-complete problem (under both definitions) such as for example the complement of the boolean satisfiability problem that is also NP-complete (under both definitions). This implies that NP = co-NP as is shown in the proof in the article on co-NP. Although the question of NP = co-NP is an open question it is considered unlikely and therefore it is also unlikely that the two definitions of NP-completeness are equivalent.
Another type of reduction that is also often used to define NP-completeness is the logarithmic-space many-one reduction which is a many-one reduction that can be computed with only a logarithmic amount of space. Since every computation that can be done in logarithmic space can also be done in polynomial time it follows that if there is a logarithmic-space many-one reduction then there is also a polynomial-time many-one reduction. This type of reduction is more refined than the more usual polynomial-time many-one reductions and it allows us to distinguish more classes such as P-complete. Whether under these types of reductions the definition of NP-complete changes is still an open problem.
See also
References
- Garey, M. and D. Johnson, Computers and Intractability; A Guide to the Theory of NP-Completeness, 1979. ISBN 0716710455 (This book is a classic, developing the theory, then cataloging many NP-Complete problems)
- S. A. Cook, The complexity of theorem proving procedures, Proceedings, Third Annual ACM Symposium on the Theory of Computing, ACM, New York, 1971, 151-158
- Paul E. Dunne. An Annotated List of Selected NP-complete Problems (http://www.csc.liv.ac.uk/~ped/teachadmin/COMP202/annotated_np.html). The University of Liverpool, Dept of Computer Science, COMP202.
- Pierluigi Crescenzi, Viggo Kann, Magnús Halldórsson, Marek Karpinski, and Gerhard Woeginger. A compendium of NP optimization problems (http://www.nada.kth.se/~viggo/problemlist/compendium.html). KTH NADA. Stockholm.
- Computational Complexity of Games and Puzzles (http://www.ics.uci.edu/~eppstein/cgt/hard.html)
- Tetris is Hard, Even to Approximate (http://arxiv.org/abs/cs.CC/0210020)
- Minesweeper is NP-complete! (http://for.mat.bham.ac.uk/R.W.Kaye/minesw/ordmsw.htm)
| Important complexity classes (more) |
| P | NP | Co-NP | NP-C | Co-NP-C | NP-hard | UP | #P | #P-C | L | NC | P-C |
| PSPACE | PSPACE-C | EXPTIME | EXPSPACE | BQP | BPP | RP | ZPP | PCP | IP | PH |
de:NP-Vollständigkeit es:NP-completo he:NP-שלמה ja:NP完全 pl:Problem NP zupełny