Truncated octahedron
|
|
| Truncated octahedron | |
|---|---|
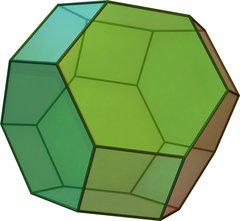 Click on picture for large version. Click here for spinning version. | |
| Type | Archimedean |
| Faces | 6 squares 8 hexagons |
| Edges | 36 |
| Vertices | 24 |
| Vertex configuration | 4,6,6 |
| Symmetry group | octahedral (Oh) |
| Dual polyhedron | tetrakis hexahedron |
| Properties | convex, semi-regular (vertex-uniform), zonohedron |
The truncated octahedron is an Archimedean solid. It has 8 regular hexagonal faces, 6 regular square faces, 24 vertices and 36 edges. Since each of its faces has point symmetry (or 180° rotational symmetry), the truncated octahedron is a zonohedron.
Missing image
Truncated_octahedron_flat.png
image:Truncated octahedron flat.png
Canonical coordinates for the vertices of a truncated octahedron centered at the origin are (±2, ±1, 0), (0, ±2, ±1), (±1, 0, ±2), (±1, ±2, 0), (0, ±1, ±2), (±2, 0, ±1), note that the coordinates form a lot of rectangles parallel with the coordinate system axes.
Truncated octahedra are able to tessellate 3-dimensional space, forming an Andreini tessellation. This tessellation can also be seen as the Voronoi tessellation of the body-centred cubic lattice.
See also
External links
- The Uniform Polyhedra (http://www.mathconsult.ch/showroom/unipoly/)
- Virtual Reality Polyhedra (http://www.georgehart.com/virtual-polyhedra/vp.html) The Encyclopedia of Polyhedra

