Triangle wave
|
|
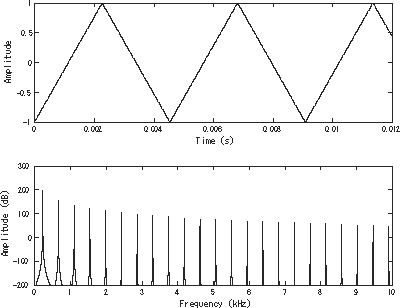
A triangle wave is a waveform named for its triangular shape.
 | ||
|
Like a square wave, the triangle wave contains only odd harmonics. However, the higher harmonics roll off much faster than in a square wave (proportional to the inverse square of the harmonic number as opposed to just the inverse), and so its sound is smoother than a square wave and is nearer to that of a sine wave.
It is possible to approximate a triangle wave with additive synthesis by adding odd harmonics of the fundamental, multiplying every (4n-1)th harmonic by -1 (or changing its phase by <math>\pi<math>), and rolling off the harmonics by the inverse square of their relative frequency to the fundamental.
This infinite Fourier series converges to the triangle wave:
- <math>x_{triangle}(t) = \frac {8}{\pi^2} \sum_{k=1}^\infty \sin \left(\frac {k\pi}{2}\right)\frac{ \sin (kt)}{k^2}<math>
See also:
