Sawtooth wave
|
|
The sawtooth wave is a kind of basic waveform. It is named a sawtooth based on its resemblance to the teeth on the blade of a saw.
 | ||
|
The piecewise linear function y = x - floor(x) is an example of a sawtooth wave with period 1.
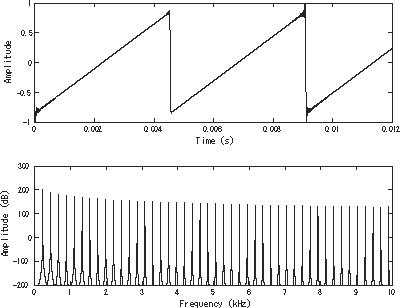
A sawtooth wave's sound is harsh and clear and its spectrum contains both even and odd harmonics of the fundamental frequency. Because it contains all the integer harmonics, it is one of the best waveforms to use for constructing other sounds, particularly strings, using subtractive synthesis.
A sawtooth can be constructed using additive synthesis. The infinite Fourier series
- <math>x_{sawtooth}(t) = \frac {2}{\pi}\sum_{k=1}^{\infin} \frac {\sin kt}{k} <math>
converges to a sawtooth wave. In digital synthesis, the series is only summed over n such that the highest harmonic, Nmax, is less than the Nyquist frequency (half the sampling Frequency). This summation can generally be more efficiently calculated using the Fast Fourier transform. If the waveform is digitally created directly in the time domain using a non-bandlimited form, such as y = x - floor(x), infinite harmonics are sampled and the resulting tone contains aliasing distortion.
An audio demonstration of a sawtooth played at 440 Hz (A4) and 880 Hz (A5) and 1760 Hz (A6) is available below. Both bandlimited (non-aliased) and aliased tones are presented.
- Sawtooth aliasing demo {440 Hz bandlimited, 440 Hz aliased, 880 Hz bandlimited, 880 Hz aliased, 1760 Hz bandlimited, 1760 Hz aliased}
