Super ellipse
|
|
A superellipse is a geometrical figure which in a cartesian coordinate system can be described as the set of all points (x, y) with
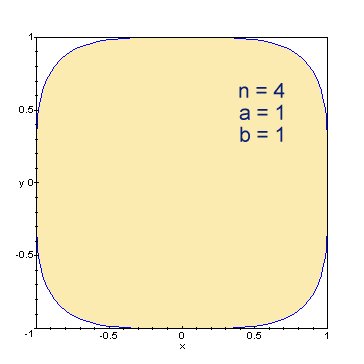
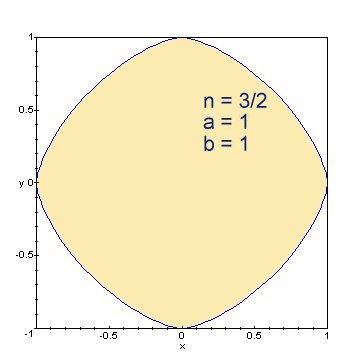
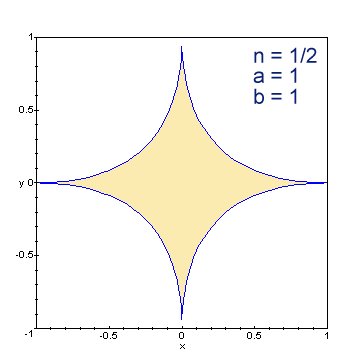
- <math>\left|\frac{x}{a}\right|^n\! + \left|\frac{y}{b}\right|^n\! = 1<math>
where <math>n > 0<math> and <math>a<math> and <math>b<math> are the radii of the oval shape. The case <math>n = 2<math> yields an ordinary ellipse; increasing <math>n<math> beyond 2 yields the hyperellipses, which increasingly resemble rectangles; decreasing <math>n<math> below 2 yields hypoellipses which develop pointy corners in the <math>x<math> and <math>y<math> directions and increasingly resemble crosses.
- <math>x\left(\theta\right) = \plusmn acos^\frac{2}{n} \left(\theta\right),<math>
- <math>y\left(\theta\right) = \plusmn bsin^\frac{2}{n} \left(\theta\right);<math>
- <math>0 \le \theta < \frac{\pi}{2}.<math>
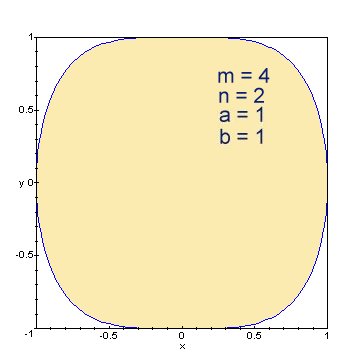
The superellipse is further generalized as:
- <math>\left|\frac{x}{a}\right|^m + \left|\frac{y}{b}\right|^n = 1; m, n > 0.<math>
Though he is often credited with its invention, the Danish poet and scientist Piet Hein (1905-1996) did not discover the super-ellipse. The general Cartesian notation of the form comes from the French mathematician Gabriel Lamé (1795–1870) who generalized the equation for the ellipse.
However, Piet Hein did popularize the use of the superellipse in architecture, urban planning, and furniture making, and he did invent the super-egg or super-ellipsoid by starting with the superellipse
- <math>\left|\frac{x}{4}\right|^{2.5} + \left|\frac{y}{3}\right|^{2.5} = 1<math>
and revolving it about the <math>x<math>-axis. Unlike a regular ellipsoid, the super-ellipsoid can stand upright on a flat surface.
City planners in Stockholm, Sweden needed a solution for a roundabout in their old city square Sergels Torg. Piet Hein's superellipse provided the needed aesthetic and practical solution. In 1969, negotiators in Paris for the Vietnam War could not agree on the shape of the negotiating table. Piet Hein designed a huge superelliptical table which accommodated all parties. The superellipse was used for the shape of the 1968 Azteca Olympic Stadium [1] (http://www.mexico-city-mexico.com), [2] (http://www.worldstadiums.com/stadium_pictures/north_america/mexico/mexico_city_azteca.shtml) in Mexico City.
- Man is the animal that draws lines which he himself then stumbles over. In the whole pattern of civilization there have been two tendencies, one toward straight lines and rectangular patterns and one toward circular lines. There are reasons, mechanical and psychological, for both tendencies. Things made with straight lines fit well together and save space. And we can move easily — physically or mentally — around things made with round lines. But we are in a straitjacket, having to accept one or the other, when often some intermediate form would be better. To draw something freehand — such as the patchwork traffic circle they tried in Stockholm — will not do. It isn't fixed, isn't definite like a circle or square. You don't know what it is. It isn't esthetically satisfying. The super-ellipse solved the problem. It is neither round nor rectangular, but in between. Yet it is fixed, it is definite — it has a unity. —Piet Hein
More recently, superellipses formed the base of a new technology developed by Johan Gielis (http://www.geniaal.be) and Bert Beirinckx (http://users.skynet.be/bert.beirinckx) in the late 1990s. They baptized this new technology the "Superformula (http://www.genicap.com)," which enables shape definition of all kinds of shapes in both 2D and 3D, thus applying the philosophy of Piet Hein.
See also
- Ellipse
- Ellipsoid, a higher-dimensional analogue of an ellipse
- Spheroid, the ellipsoids obtained by rotating an ellipse about its major or minor axis
- Hyperbola
- Parabola
- Ellipsis
References
- Gardner, Martin: Piet Hein's Superellipse. - in Gardner, Martin: Mathematical Carnival. A New Round-Up of Tantalizers and Puzzles from Scientific American. New York: Vintage, 1977, pp. 240-254.
- Johan Gielis: Inventing the circle. The geometry of nature. - Antwerpen : Geniaal Press, 2003. - ISBN 9080775614
External links
- Superellipse (MathWorld) (http://mathworld.wolfram.com/Superellipse.html)
- Lamé's Super Ellipse (Java-Applet) (http://www.activeart.de/dim-shops/training/SuperEllipse)
- Super Ellipsoid (Java-Applet) (http://www.activeart.de/dim-shops/training/SuperEllipse3D)da:Superellipse