Spheroid
|
|
A spheroid is a quadric surface in three dimensions obtained by rotating an ellipse about one of its principal axes. If the ellipse is rotated about its major axis, the surface is called a prolate spheroid (similar to the shape of a rugby ball or cigar). If the minor axis is chosen, the surface is called an oblate spheroid (similar to the shape of the planet Earth).
A spheroid can also be characterised as an ellipsoid having two equal semi-axes, as represented by the equation
- <math>\frac{x^2}{a^2}+\frac{y^2}{b^2}+\frac{z^2}{b^2}=1<math>
A prolate spheroid has one semiaxis longer than the other two, (a > b); an oblate spheroid has two equal semiaxes that are longer than the third one(a < b) and can resemble a disk.
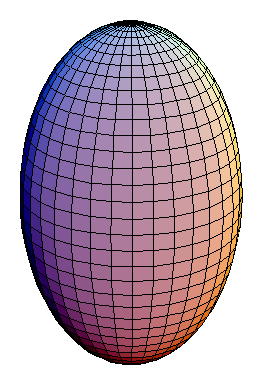
| Missing image OblateSpheroid.PNG Image:OblateSpheroid.PNG
|
The sphere is a special case of the spheroid in which the generating ellipse is a circle.
Volume
Prolate spheroid:
- volume is <math>\frac{4}{3}\pi a b^2<math>
Oblate spheroid:
- volume is <math>\frac{4}{3}\pi a^2 b<math>
where
- a is the major axis length
- b is the minor axis length
Surface area
A prolate spheroid has surface area
- <math>\pi\left(2 a^2 + \frac{b^2}{e} \ln\left(\frac{1+e}{1-e}\right) \right).<math>
An oblate spheroid has surface area
- <math>2\pi b\left(b + a \frac{\arcsin{e}}{e}\right)<math>.
Here e is the eccentricity of the ellipse, defined as
- <math>\left(1-(b^2/a^2)\right)^{1/2}.<math>de:Rotationsellipsoid
