Superconductivity
|
|

Superconductivity is a phenomenon occurring in certain materials at low temperatures, characterised by the complete absence of electrical resistance and the damping of the interior magnetic field (the Meissner effect.)
In conventional superconductors, superconductivity is caused by a force of attraction between certain conduction electrons arising from the exchange of phonons, which causes the conduction electrons to exhibit a superfluid phase composed of correlated pairs of electrons. There also exists a class of materials, known as unconventional superconductors, that exhibit superconductivity but whose physical properties contradict the theory of conventional superconductors. In particular, the so-called high-temperature superconductors superconduct at temperatures much higher than should be possible according to the conventional theory (though still far below room temperature.) There is currently no complete theory of high-temperature superconductivity.
Superconductivity occurs in a wide variety of materials, including simple elements like tin and aluminium, various metallic alloys, some heavily-doped semiconductors, and certain ceramic compounds containing planes of copper and oxygen atoms. The latter class of compounds, known as the cuprates, are high-temperature superconductors. Superconductivity does not occur in noble metals like gold and silver, nor in most ferromagnetic metals, though a number of materials displaying both superconductivity and ferromagnetism has been discovered in recent years.
| Contents |
Elementary properties of superconductors
Most of the physical properties of superconductors vary from material to material, such as the heat capacity and the critical temperature at which superconductivity is destroyed. On the other hand, there is a class of properties that are independent of the underlying material. For instance, all superconductors have exactly zero resistivity to low applied currents when there is no magnetic field present. The existence of these "universal" properties imply that superconductivity is a thermodynamic phase, and thus possess certain distinguishing properties which are largely independent of microscopic details.
Zero electrical resistance
Suppose we were to attempt to measure the electrical resistance of a piece of superconductor. The simplest method is to place the sample in an electrical circuit, in series with a voltage (potential difference) source V (such as a battery), and measure the resulting current. If we carefully account for the resistance R of the remaining circuit elements (such as the leads connecting the sample to the rest of the circuit, and the source's internal resistance), we would find that the current is simply V/R. According to Ohm's law, this means that the resistance of the superconducting sample is zero.
Superconductors are also able to maintain a current with no applied voltage whatsoever, a property exploited in superconducting electromagnets such as those found in MRI machines. Experiments have demonstrated that currents in superconducting coils can persist for years without any measurable degradation. Experimental evidence points to a current lifetime of at least 100,000 years, and theoretical estimates for the lifetime of persistent current exceed the lifetime of the universe.
In a normal conductor, an electrical current may be visualized as a fluid of electrons moving across a heavy ionic lattice. The electrons are constantly colliding with the ions in the lattice, and during each collision some of the energy carried by the current is absorbed by the lattice and converted into heat (which is essentially the vibrational kinetic energy of the lattice ions.) As a result, the energy carried by the current is constantly being dissipated. This is the phenomenon of electrical resistance.
The situation is different in a superconductor. In a conventional superconductor, the electronic fluid cannot be resolved into individual electrons, instead consisting of bound pairs of electrons known as Cooper pairs. This pairing is caused by an attractive force between electrons from the exchange of phonons. Due to quantum mechanics, the energy spectrum of this Cooper pair fluid possesses an energy gap, meaning there is a minimum amount of energy ΔE that must be supplied in order to excite the fluid. Therefore, if ΔE is larger than the thermal energy of the lattice (given by kT, where k is Boltzmann's constant and T is the temperature), the fluid will not be scattered by the lattice. The Cooper pair fluid is thus a superfluid, meaning it can flow without energy dissipation.
In a class of superconductors known as type II superconductors (including all known high-temperature superconductors), an extremely small amount of resistivity appears when an electrical current is applied in conjunction with a strong magnetic field (which may be caused by the electrical current). This is due to the motion of vortices in the electronic superfluid, which dissipates some of the energy carried by the current. If the current is sufficiently small, the vortices are stationary, and the resistivity vanishes. The resistance due to this effect is tiny compared with that of non-superconducting materials, but must be taken into account in sensitive experiments.
Superconducting phase transition
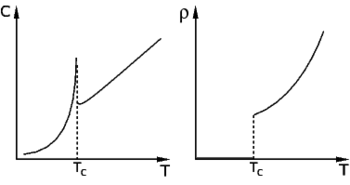
In superconducting materials, the characteristics of superconductivity appear when the temperature T is lowered below a critical temperature Tc. The value of this critical temperature varies from material to material. Conventional superconductors usually have critical temperatures ranging from less than 1K to around 20K. Solid mercury, for example, has a critical temperature of 4.2K. As of 2001, the highest critical temperature found for a conventional superconductor is 39 K for magnesium diboride (MgB2), although this material displays enough exotic properties that there is doubt about classifying it as a "conventional" superconductor. Cuprate superconductors can have much higher critical temperatures: YBa2Cu3O7, one of the first cuprate superconductors to be discovered, has a critical temperature of 92 K, and mercury-based cuprates have been found with critical temperatures in excess of 130 K. The explanation for these high critical temperatures remains unknown. (Electron pairing due to phonon exchanges explains superconductivity in conventional superconductors, but it does not explain superconductivity in the newer superconductors that have a very high Tc.)
The onset of superconductivity is accompanied by abrupt changes in various physical properties, which is the hallmark of a phase transition. For example, the electronic heat capacity is proportional to the temperature in the normal (non-superconducting) regime. At the superconducting transition, it suffers a discontinuous jump and thereafter ceases to be linear. At low temperatures, it varies instead as e−α/T for some constant α. (This exponential behavior is one of the pieces of evidence for the existence of the energy gap.)
The order of the superconducting phase transition is still a matter of debate. It had long been thought that the transition is second-order, meaning there is no latent heat. However, recent calculations have suggested that it may actually be weakly first-order due to the effect of long-range fluctuations in the electromagnetic field.
Meissner effect
When a superconductor is placed in a weak external magnetic field H, the field penetrates for only a short distance λ, called the penetration depth, after which it decays rapidly to zero. This is called the Meissner effect. For most superconductors, the penetration depth is on the order of a hundred nm.
The Meissner effect is sometimes confused with the "perfect diamagnetism" one would expect in a perfect electrical conductor: according to Lenz's law, when a changing magnetic field is applied to a conductor, it will induce an electrical current in the conductor that creates an opposing magnetic field. In a perfect conductor, an arbitrarily large current can be induced, and the resulting magnetic field exactly cancels the applied field.
The Meissner effect is distinct from perfect diamagnetism because a superconductor expels all magnetic fields, not just those that are changing. Suppose we have a material in its normal state, containing a constant internal magnetic field. When the material is cooled below the critical temperature, we would observe the abrupt expulsion of the internal magnetic field, which we would not expect based on Lenz's law. A conductor in a static field, such as the dome of a Van de Graaff generator, will have a field within itself, even if there is no net charge in the interior.
The Meissner effect was explained by London and London, who showed that the electromagnetic free energy in a superconductor is minimized provided
- <math> \nabla^2\mathbf{H} = \lambda^{-2} \mathbf{H}\, <math>
where H is the magnetic field and λ is the penetration depth. This equation, which is known as the London equation, predicts that the magnetic field in a superconductor decays exponentially from whatever value it possesses at the surface.
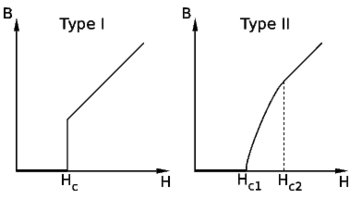
The Meissner effect breaks down when the applied magnetic field is too large. Superconductors can be divided into two classes according to how this breakdown occurs. In Type I superconductors, superconductivity is abruptly destroyed when the strength of the applied field rises above a critical value Hc. Depending on the geometry of the sample, one may obtain an intermediate state consisting of regions of normal material carrying a magnetic field mixed with regions of superconducting material containing no field. In Type II superconductors, raising the applied field past a critical value Hc1 leads to a mixed state in which an increasing amount of magnetic flux penetrates the material, but there remains no resistance to the flow of electrical current as long as the current is not too large. At a second critical field strength Hc2, superconductivity is destroyed. The mixed state is actually caused by vortices in the electronic superfluid, sometimes called "fluxons" because the flux carried by these vortices is quantized. Most pure elemental superconductors (except niobium, technetium, vanadium and carbon nanotubes) are Type I, while almost all impure and compound superconductors are Type II.
Theories of superconductivity
Since the discovery of superconductivity, great efforts have been devoted to finding out how and why it works. During the 1950s, theoretical condensed matter physicists arrived at a solid understanding of "conventional" superconductivity, through a pair of remarkable and important theories: the phenomenological Ginzburg-Landau theory (1950) and the microscopic BCS theory (1957). Generalisations of these theories form the basis for understanding the closely related phenomenon of superfluidity, but the extent to which similar generalisations can be applied to unconventional superconductors as well is still controversial.
History of superconductivity
Main article : History of superconductivity
Superconductivity was discovered in 1911 by Heike Kamerlingh Onnes, who was studying the resistivity of solid mercury at cryogenic temperatures using the recently-discovered liquid helium as a refrigerant. At the temperature of 4.2 K, he observed that the resistivity abruptly disappeared. For this discovery, he was awarded the Nobel Prize in Physics in 1913.
In subsequent decades, superconductivity was found in several other materials. In 1913, lead was found to superconduct at 7 K, and in 1941 niobium nitride was found to superconduct at 16 K.
The next important step in understanding superconductivity occurred in 1933, when Meissner and Ochsenfeld discovered that superconductors expelled applied magnetic fields, a phenomenon which has come to be known as the Meissner effect. In 1935, F. and H. London showed that the Meissner effect was a consequence of the minimization of the electromagnetic free energy carried by superconducting current.
In 1950, the phenomenological Ginzburg-Landau theory of superconductivity was devised by Landau and Ginzburg. This theory, which combined Landau's theory of second-order phase transitions with a Scrödinger-like wave equation, had great success in explaining the macroscopic properties of superconductors. In particular, Abrikosov showed that Ginzburg-Landau theory predicts the division of superconductors into the two categories now referred to as Type I and Type II. Abrikosov and Ginzburg were awarded the 2003 Nobel Prize for their work (Landau having died in 1968.)
Also in 1950, Maxwell and Reynolds et. al. found that the critical temperature of a superconductor depends on the isotopic mass of the constituent element. This important discovery pointed to the electron-phonon interaction as the microscopic mechanism responsible for superconductivity.
The complete microscopic theory of superconductivity was finally proposed in 1957 by Bardeen, Cooper, and Schrieffer. This BCS theory explained the superconducting current as a superfluid of Cooper pairs, pairs of electrons interacting through the exchange of phonons. For this work, the authors were awarded the Nobel Prize in 1972.
The BCS theory was set on a firmer footing in 1958, when Bogoliubov showed that the BCS wavefunction, which had originally been derived from a variational argument, could be obtained using a canonical transformation of the electronic Hamiltonian. In 1959, Gor'kov showed that the BCS theory reduced to the Ginzburg-Landau theory close to the critical temperature.
In 1962, the first commercial superconducting wire, a niobium-titanium alloy, was developed by researchers at Westinghouse. In the same year, Josephson made the important theoretical prediction that a supercurrent can flow between two pieces of superconductor separated by a thin layer of insulator. This phenomenon, now called the Josephson effect, is exploited by superconducting devices such as SQUIDs. It is used in the most accurate available measurements of the magnetic flux quantum h/e, and thus (coupled with the quantum Hall resistivity) for Planck's constant h. Josephson was awarded the Nobel Prize for this work in 1973.
Until 1986, physicists had believed that BCS theory forbade superconductivity at temperatures above about 30 K. In that year, Bednorz and Mueller discovered superconductivity in a lanthanum-based cuprate perovskite material, which had a transition temperature of 35 K (Nobel Prize in Physics, 1987). It was shortly found that replacing the lanthanum with yttrium, i.e. making YBCO, raised the critical temperature to 92 K, which was important because liquid nitrogen could then be used as a refrigerant (at atmospheric pressure, the boiling point of nitrogen is 77 K.) This is important commercially because liquid nitrogen can be produced cheaply on-site with no raw materials, and is not prone to some of the problems (solid air plugs, etc) of helium in piping. Many other cuprate superconductors have since been discovered, and the theory of superconductivity in these materials is one of the major outstanding challenges of theoretical condensed matter physics.
Technological applications of superconductivity
There have been many technological innovations based on superconductivity. Superconductors are used to make the most powerful electromagnets known to man, including those used in MRI machines and the beam-steering magnets used in particle accelerators. They are also used to make SQUIDs (superconducting quantum interference devices), the most sensitive magnetometers known.
Superconductors have also been used to make digital circuits (e.g. based on the Rapid Single Flux Quantum technology) and microwave filters for mobile phone base stations.
Many promising applications of superconductivity have been stalled by the impracticality of maintaining large systems (e.g. long stretches of cable) at cryogenic temperatures. These problems may soon be alleviated with the continued development of high temperature superconductors, as these can be cooled by using liquid nitrogen rather than liquid helium (which is much more expensive and difficult to handle) or by using cryocoolers. However, the currently known high-temperature superconductors are brittle ceramics which are not easily turned into wires or other useful shapes. Promising future applications include high-performance transformers, power storage devices, electric power transmission, electric motors (e.g. for vehicle propulsion), and magnetic levitation devices.
Superconductors in science fiction
Superconductivity has long been a staple of science fiction. One of the first mentions of the phenomenon occurred in Robert Heinlein's novel Beyond This Horizon (1942). Notably, the use of a fictional room temperature superconductor was a major plot point in the Ringworld novels by Larry Niven, first published in 1970.
Superconductivity is a popular device in science fiction due to the simplicity of the underlying concept - zero electrical resistance - and the rich technological possibilities. For example, superconducting magnets could be used to generate the powerful magnetic fields used by Bussard ramjets, a type of spacecraft commonly encountered in science fiction. The most troublesome property of real superconductors, the need for cryogenic cooling, is often circumvented by postulating the existence of room temperature superconductors. Many stories attribute additional properties to their fictional superconductors, ranging from infinite heat conductivity in Niven's novels (real superconductors conduct heat poorly, though superfluid helium has immense but finite heat conductivity) to teleportation in the Stargate movie and TV series.
In the movie Terminator 2 : Judgement Day, the CPU of the T800 destroyed in Terminator 1 is found to be superconductive at room temperature.
Links and references
Selected references
Papers
- H.K. Onnes, Commun. Phys. Lab. 12, 120 (1911)
- W. Meissner and R. Oschenfeld, Naturwiss. 21, 787 (1933)
- F. London and H. London, Proc. R. Soc. London A149, 71 (1935)
- V.L. Ginzburg and L.D. Landau, Zh. Eksp. Teor. Fiz. 20, 1064 (1950)
- E.Maxwell, Phys. Rev. 78, 477 (1950)
- C.A. Reynolds et. al., Phys. Rev. 78, 487 (1950)
- J. Bardeen, L.N. Cooper, and J.R. Schrieffer, Phys. Rev. 108, 1175 (1957)
- N.N. Bogoliubov, Zh. Eksp. Teor. Fiz. 34, 58 (1958)
- L.P. Gor'kov, Zh. Eksp. Teor. Fiz. 36, 1364 (1959)
- B.D. Josephson, Phys. Lett. 1, 251 (1962)
- J.G. Bednorz and K.A. Mueller, Z. Phys. B64, 189 (1986)
External links
- US, EREN: superconductivity (http://www.eren.doe.gov/superconductivity/)
- superconductors.org (http://www.superconductors.org/)
- Introduction to superconductivity (http://www.ornl.gov/reports/m/ornlm3063r1/pt1.html)
See also
bg:Свръхпроводимост da:Superleder de:Supraleiter es:Superconductividad fr:Supraconductivité it:Superconduzione he:מוליכות על nl:Supergeleiding ja:超伝導 pl:Nadprzewodnictwo ro:Superconductivitate sr:Суперпроводност sl:Superprevodnost sv:Supraledare vi:Siêu dẫn zh:超导现象