Substitution cipher
|
|
In cryptography, a substitution cipher is a method of encryption by which units of plaintext are substituted with ciphertext according to a regular system; the "units" may be single letters (the most common), pairs of letters, triplets of letters, mixtures of the above, and so forth. The receiver deciphers the text by performing an inverse substitution.
Substitution ciphers can be compared with transposition ciphers. In a transposition cipher, units of the plaintext are rearranged in a different and usually quite complex order, but the units themselves are left unchanged. By contrast, in a substitution cipher, the units of the plaintext are retained in the same sequence in the ciphertext, but the units themselves are altered.
There are a number of different types of substitution cipher. If the cipher operates on single letters, it is termed a simple substitution cipher; a cipher that operates on larger groups of letters is termed polygraphic. A monoalphabetic cipher uses fixed substitution over the entire message, whereas a polyalphabetic cipher uses a number of substitutions at different times in the message—such as with homophones, where a unit from the plaintext is mapped to one of several possibilities in the ciphertext.
| Contents |
Simple substitution
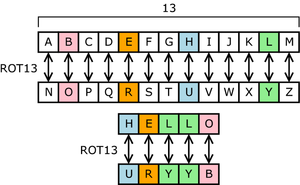
Substitution over a single letter—simple substitution—can be demonstrated by writing out the alphabet in some order to represent the substitution. This is termed a substitution alphabet. The cipher alphabet may be shifted or reversed (creating the Caesar and Atbash ciphers, respectively) or scrambled in a more complex fashion, in which case it is called a mixed alphabet or deranged alphabet. Traditionally, mixed alphabets are created by first writing out a keyword, then all the remaining letters.
Examples
Using this system, the keyword "zebras" gives us the following alphabets:
| Plaintext alphabet: | abcdefghijklmnopqrstuvwxyz |
| Ciphertext alphabet: | ZEBRASCDFGHIJKLMNOPQTUVWXY |
A message of
flee at once. we are discovered!
enciphers to
SIAA ZQ LKBA. VA ZOA RFPBLUAOAR!
Traditionally, the ciphertext is written out in blocks of fixed length, omitting punctuation and spaces; this is done to help avoid transmission errors and to disguise word boundaries from the plaintext. These blocks are called "groups", and sometimes a "group count" (i.e., the number of groups) is given as an additional check. Five letter groups are traditional, dating from when messages used to be transmitted by telegraph:
SIAAZ QLKBA VAZOA RFPBL UAOAR
If the length of the message happens not to be divisible by five, it may be padded at the end with "nulls". These can be any characters that decrypt to obvious nonsense, so the receiver can easily spot them and discard them.
The ciphertext alphabet is sometimes different from the plaintext alphabet; for example, in the pigpen cipher, the ciphertext consists of a set of symbols derived from a grid. For example:
A-pigpen-message.png
An example pigpen message
Such features make little difference to the security of a scheme, however — at the very least, any set of strange symbols can be transcribed back into an A-Z alphabet and dealt with as normal.
Security for simple substitution ciphers
A disadvantage of this method of derangement is that the last letters of the alphabet (which are mostly low frequency) tend to stay at the end. A stronger way of constructing a mixed alphabet is to perform a columnar transposition on the ordinary alphabet using the keyword, but this is not often done.
Although the number of possible keys is very large (<math>26! \approx 2^{88.4}<math>, or about 88 bits), this cipher is not very strong, being easily broken. Provided the message is of reasonable length (see below), the cryptanalyst can deduce the probable meaning of the most common symbols by analysing the frequency distribution of the ciphertext—frequency analysis. This allows formation of partial words, which can be tentatively filled in, progressively expanding the (partial) solution (see frequency analysis for a demonstration of this). In some cases, underlying words can also be determined from the pattern of their letters; for example, attract, osseous, and words with those two as the root are the only common English words with the pattern ABBCADB. Many people solve such ciphers for recreation, as with cryptogram puzzles in the newspaper.
According to the unicity distance of English, 27.6 letters of ciphertext are required to crack a mixed alphabet simple substitution. In practice, typically about 50 letters are needed, although some messages can be broken with fewer if unusual patterns are found. In other cases, the plaintext can be contrived to have a nearly flat frequency distribution, and much longer plaintexts will then be required.
Homophonic substitution
Babington_postscript.jpg
An early attempt to increase the difficulty of frequency analysis attacks on substitution ciphers was to disguise plaintext letter frequencies by homophony. In these ciphers, plaintext letters map to more than one ciphertext symbol. Usually, the highest-frequency plaintext symbols are given more equivalents than lower frequency letters. In this way, the frequency distribution is flattened, making analysis more difficult.
Since more than 26 characters will be required in the ciphertext alphabet, various solutions are employed to invent larger alphabets. Perhaps the simplest is to use a numeric substitution 'alphabet'. Another method consists of simple variations on the existing alphabet; uppercase, lowercase, upside down, etc. More artistically, though not necessarily more securely, some homophonic ciphers employed wholly invented alphabets of fanciful symbols. (See Poe's The Gold Bug for a literary example; cf. the Voynich manuscript.)
An interesting variant is the nomenclator. Named after the public official who announced the titles of visiting dignitaries, this cipher combined a small codebook with large homophonic substitution tables. Originally the code was restricted to the names of important people, hence the name of the cipher; in later years it covered many common words and place names as well. The symbols for whole words (codewords in modern parlance) and letters (cipher in modern parlance) were not distinguished in the ciphertext. The Rossignols' Great Cypher used by Louis XIV of France was one; after it went out of use, messages in French archives were unbreakable for several hundred years.
Nomenclators were the standard fare of diplomatic correspondence, espionage, and advanced political conspiracy from the early fifteenth century to the late eighteenth century; most conspirators were and have remained less cryptographically sophisticated. Although government intelligence cryptanalysts were systematically breaking nomenclators by the mid-sixteenth century, and superior systems had been available since 1467, the usual response to cryptanalysis was simply to make the tables larger. By the late eighteenth century, when the system was beginning to die out, some nomenclators had 50,000 symbols!
Nevertheless, not all nomenclators were broken; today, cryptanalysis of archived ciphertexts remains a fruitful area of historical research.
The book cipher and straddling checkerboard are types of homophonic cipher.
Polyalphabetic substitution
- Main article: Polyalphabetic cipher
Polyalphabetic substitution ciphers were first described in 1467 by Leone Battista Alberti in the form of disks. Johannes Trithemius, in his book Steganographia (Ancient Greek for "hidden writing") introduced the now more standard form of a tableau (see below; ca. 1500 but not published until much later). A more sophisticated version using mixed alphabets was described in 1563 by Giovanni Battista della Porta in his book, De Furtivis Literarum Notis (Latin for "On concealed characters in writing").
In a polyalphabetic cipher, multiple cipher alphabets are used. To facilitate encryption, all the alphabets are usually written out in a large table, traditionally called a tableau. The tableau is usually 26×26, so that 26 full ciphertext alphabets are available. The method of filling the tableau, and of choosing which alphabet to use next, defines the particular polyalphabetic cipher. All such ciphers are easier to break than once believed, as substitution alphabets are repeated for sufficiently large plaintexts.
One of the most popular was that of Blaise de Vigenčre. First published in 1585, it was considered unbreakable until 1863, and indeed was commonly called le chiffre indéchiffrable (French for "indecipherable cipher").
In the Vigenčre cipher, the first row of the tableau is filled out with a copy of the plaintext alphabet, and successive rows are simply shifted one place to the left. (Such a simple tableau is called a tabula recta, and mathematically corresponds to adding the plaintext and key letters, modulo 26.) A keyword is then used to choose which ciphertext alphabet to use. Each letter of the keyword is used in turn, and then they are repeated again from the beginning. So if the keyword is 'CAT', the first letter of plaintext is enciphered under alphabet 'C', the second under 'A', the third under 'T', the fourth under 'C' again, and so on. In practice, Vigenère keys were often phrases several words long.
In 1863, Friedrich Kasiski published a method (probably discovered secretly and independently before the Crimean War by Charles Babbage) which enabled the calculation of the length of the keyword in a Vigenère ciphered message. Once this was done, ciphertext letters that had been enciphered under the same alphabet could be picked out and attacked separately as a number of semi-independent simple substitutions - complicated by the fact that within one alphabet letters were separated and did not form complete words, but simplified by the fact that usually a tabula recta had been employed.
As such, even today a Vigenère type cipher should theoretically be difficult to break if mixed alphabets are used in the tableau, if the keyword is random, and if the total length of ciphertext is less than 27.6 times the length of the keyword. These requirements are rarely understood in practice, and so Vigenère enciphered message security is usually less than might have been.
Other notable polyalphabetics include:
- The Gronsfeld cipher. This is identical to the Vigenère except that only 10 alphabets are used, and so the "keyword" is numerical.
- The Beaufort cipher. This is practically the same as the Vigenère, except the tabula recta is replaced by a backwards one, mathematically equivalent to ciphertext = key - plaintext. This operation is self-inverse, so that exactly the same table is used in exactly the same way, for both encryption and decryption.
- The autokey cipher, which mixes plaintext in to the keying to avoid periodicity in the key.
- The running key cipher, where the key is made very long by using a passage from a book or similar text.
Modern stream ciphers can also be seen, from a sufficiently abstract perspective, to be a form of polyalphabetic cipher in which all the effort has gone into making the keystream as long and unpredictable as possible.
Polygraphic substitution
In a polygraphic substitution cipher, plaintext letters are substituted for in larger groups (typically pairs, making a digraphic cipher), instead of substituting letters individually. The advantage of this is first that the frequency distribution of digraphs is much flatter than that of individual letters (though not actually flat in real languages; for example, 'TH' is much more common than 'XQ' in English). Second, the larger number of symbols requires correspondingly more ciphertext to productively analyse letter frequencies.
Because <math>26^2 = 676<math>, to substitute pairs with a substitution alphabet would take an alphabet 676 symbols long—which would be rather cumbersome. (Actually, not every combination would need to be created, or rare combinations could be split into individual letters, but this is negligible.) In the same De Furtivis Literarum Notis mentioned above, della Porta actually proposed such a system, with a 26 x 26 tableau filled with 676 unique glyphs. However the system was impractical and probably never actually used. Algebraic or geometric methods are typically used to construct the substitution from simple operations.
The earliest practical digraphic substitution was the so-called Playfair cipher, actually invented by Sir Charles Wheatstone in 1854. It was in military use from the Boer War through World War II. In this cipher, a 5 x 5 grid is filled with the letters of a mixed alphabet (two letters, usually I and J, are combined). A digraphic substitution is then simulated by taking pairs of letters as two corners of a rectangle, and using the other two corners as the ciphertext (see the Playfair cipher main article for a diagram). Special rules handle double letters and pairs falling in the same row or column.
Several other practical polygraphics were introduced in 1901 by Felix Delastelle, including the bifid and four-square ciphers (both digraphic) and the trifid cipher (probably the first practical trigraphic).
The Hill cipher is a polygraphic substitution which can combine much larger groups of letters simultaneously, using linear algebra. It was invented in 1929 by Lester S. Hill. Each letter is treated as a digit in base 26: A = 0, B =1, and so on. (In a variation, 3 extra symbols are added to make the basis prime.) A block of n letters is then considered as a vector of n dimensions, and multiplied by a n x n matrix, modulo 26. The components of the matrix are the key, and should be random provided that the matrix is invertible in <math>\mathbb{Z}_{26}^n<math> (to ensure decryption is possible). Astonishingly, a Hill cipher of dimension 6 was once implemented mechanically!
Unfortunately, the Hill cipher is vulnerable to a known-plaintext attack because it is completely linear, so it must be combined with some non-linear step to defeat this attack. The combination of wider and wider weak, linear diffusive steps like a Hill cipher, with non-linear substitution steps, ultimately leads to a substitution-permutation network (e.g., a Feistel cipher), so it is possible—from this extreme perspective—to consider modern block ciphers as a type of polygraphic substitution.
Mechanical substitution ciphers
Between circa WWI and the widespread availability of computers (for some governments this was approximately the 1950s or 1960s; for other organizations it was a decade or more later; for individuals it was no earlier than 1975), mechanical implementations of polyalphabetic substitution ciphers were widely used. Several inventors had similar ideas about the same time, and rotor cipher machines were patented four times in 1919. The most important of the resulting machines was the Enigma, especially in the versions used by the German military from approximately 1930. The Allies also developed and used rotor machines (eg, SIGABA and Typex).
All of these were similar in that the substituted letter was chosen electrically from amongst the huge number of possible combinations resulting from the rotation of several letter disks. Since one or more of the disk rotated mechanically with each plaintext letter enciphered, the number of alphabets used was substantially more than astronomical. Early versions of these machine were, nevertheless, breakable. William F. Friedman of the US Army's SIS early found vulnerabilities in Hebern's rotor machine, and GC&CS's Dilwyn Knox is claimed to have broken at least one of the commercial versions of the Enigma machine well before WWII began. Traffic protected by essentially all of the German military Enigmas was broken by Allied cryptanalysts, most notably those at Bletchley Park, beginning with the German Army variant used in the early 1930s. This version was broken by inspired mathematical insight by Marian Rejewski in Poland.
No messages protected by the SIGABA and Typex machines were ever, so far as is publicly known, broken.
The one-time pad
- Main article: One-time pad
One type of substitution cipher, the one-time pad, is quite special. It was invented near the end of WWI by Gilbert Vernam and Joseph Mauborgne in the US. It was mathematically proved unbreakable by Claude Shannon, probably during WWII; his work was first published in the late 1940s. In its most common implementation, the one-time pad can be called a substitution cipher only from an unusual perspective; typically, the plaintext letter is combined (not substituted) in some manner (eg, XOR) with the key material character at that position.
The one-time pad is, in most cases, impractical as it requires that the key material be as long as the plaintext, actually random, used once and only once, and kept entirely secret from all except the sender and intended receiver. When these conditions are violated, even marginally, the one-time pad is no longer unbreakable. Soviet one-time pad messages sent from the US for a brief time during WWII used non-random key material. US cryptanalysts, beginning in the late 40s, were able to, entirely or partially, break a few thousand messages out of several hundred thousand. (See VENONA)
In a mechanical implementation, rather like the ROCKEX equipment, the one-time pad was used for messages sent on the Moscow-Washington hot line established after the Cuban missile crisis.
Substitution in modern cryptography
Substitution ciphers as discussed above, especially the older pencil-and-paper hand ciphers, are no longer in serious use. However, the cryptographic concept of substitution carries on even today. From a sufficiently abstract perspective, modern bit-oriented block ciphers (eg, DES, or AES) can be viewed as substitution ciphers on an enormously large binary alphabet. In addition, block ciphers often include smaller substitution tables called S-boxes. See also substitution-permutation network.
See also
| Classical cryptography edit (https://academickids.com:443/encyclopedia/index.php?title=Template:Classical_cryptography&action=edit) |
| Ciphers: ADFGVX | Affine | Atbash | Autokey | Bifid | Book | Caesar | Four-square | Hill | Permutation | Pigpen | Playfair | Polyalphabetic | Reihenschieber | Running key | Substitution | Transposition | Trifid | Two-square | Vigenčre
|
| Cryptanalysis: Frequency analysis | Index of coincidence |
| Misc: Cryptogram | Polybius square | Scytale | Straddling checkerboard | Tabula recta |
fr:Chiffrement de Vigenčre nl:Substitutiecijfer pl:Szyfr podstawieniowy pt:Cifra de substituiçăo
