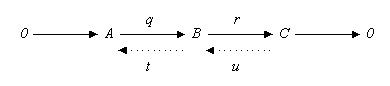
Splitting lemma
|
|
In mathematics, and more specifically in homological algebra, the splitting lemma states that the following statements regarding the below short exact sequence in any abelian category (with similar results if the objects are non-abelian groups) are equivalent:
- there exists a map t: B → A such that tq is the identity on A,
- there exists a map u: C → B such that ru is the identity on C,
- B is isomorphic to the direct sum of A and C (or a semidirect product of A by C in the case of non-abelian groups), with q being the natural injection of A and r being the natural projection onto C.
The short exact sequence is called split if any the above statements hold.
Proof
First, to show that (3) implies both (1) and (2), we assume (3) and take as t the natural projection of the direct sum (semidirect product) onto A, and take as u the natural injection of C into the direct sum (semidirect product).
To prove that (1) implies (3), first note that any member of B is in the set (ker t + im q). This follows since for all b in B, b = (b - qt(b)) + qt(b); qt(b) is obviously in im q, and (b - qt(b)) is in ker t, since
- t(b - qt(b)) = t(b) - tqt(b) = t(b) - (tq)t(b) = t(b) - t(b) = 0.
Next, the intersection of im q and ker t is 0, since if exists a in A such that q(a) = b, and t(b) = 0, then 0 = tq(a) = a; and therefore, b = 0.
(By exactness, im q = ker r, so im q is a normal subgroup of B in the case of groups.)
This proves that B is the direct sum (alternatively, a semidirect product) of im q and ker t. So, for all b in B, b can be uniquely identified by some a in A, k in ker t, such that b = q(a) + k.
By exactness, ker rq = A, and so ker r = im q. The subsequence B → C → 0 implies that f is onto; therefore for any c in C there exists some b = q(a) + k such that c = r(b) = r(q(a) + k) = r(k). Therefore, for any c in C, exists k in ker t such that c = r(k), and r(ker t) = C.
If r(k) = 0, then k is in im q; since the intersection of im q and ker t = 0, then k = 0. Therefore the restriction of the morphism f : ker t → C is an isomorphism; and ker t is isomorphic to C.
Finally, im q is isomorphic to A due to the exactness of 0 → A → B; so B is isomorphic to the direct sum (alt., a semidirect product) of A and C, which proves (3).
To show that (2) implies (3), we follow a similar argument. Any member of B is in the set ker r + im u; since for all b in B, b = (b - ur(b)) + ur(b), which is in ker r + im u. The intersection of ker r and im u is 0, since if r(b) = 0 and u(c) = b, then 0 = ru(c) = c.
By exactness, im q = ker r, and since q is an injection, im q is isomorphic to A, so A is isomorphic to ker r. Since ru is a bijection, u is an injection, and thus im u is isomorphic to C. So B is again the direct sum of A and C. In general, however, not all A will give rise to a semidirect product, though, in the case of groups. See http://planetmath.org/encyclopedia/SemidirectProduct.html on this.