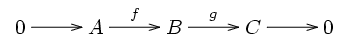Exact sequence

In mathematics, especially in homological algebra and other applications of Abelian category theory, as well as in group theory, an exact sequence is a (finite or infinite) sequence of objects and morphisms between them such that the image of one morphism equals the kernel of the next.

Contents

1 Definition 2 Example 3 Special cases 4 Facts 5 Applications of exact sequences

Definition

To be precise, fix an Abelian category (such as the category of Abelian groups or the category of vector spaces over a given field) or some other category with kernels and cokernels (such as the category of all groups). Choose an index set of consecutive integers. Then for each integer i in the index set, let A_i be an object in the category and let f_i be a morphism from A_i to A_i+1. This defines a sequence of objects and morphisms.

The sequence is exact at A_i if the image of f_i−1 is equal to the kernel of f_i:

im f_i−1 = ker f_i.

The sequence itself is exact if it is exact at each object (except possibly at the very first and the very last object, where exactness doesn't make sense).

Example

Consider the following sequence of abelian groups:

<math>0\to \Bbb{Z} \to \Bbb{Z} \to \Bbb{Z}/2\Bbb{Z}\to 0<math>

where 0 denotes the trivial abelian group with a single element, the map from Z to Z is multiplication by 2, and the map from Z to the factor group Z/2Z is given by reducing integers modulo 2. This is indeed an exact sequence:

• the image of the map 0→Z is {0}, and the kernel of multiplication by 2 is also {0}, so the sequence is exact at the first Z.
• the image of multiplication by 2 is 2Z, and the kernel of reducing modulo 2 is also 2Z, so the sequence is exact at the second Z.
• the image of reducing modulo 2 is all of Z/2Z, and the kernel of the zero map is also all of Z/2Z, so the sequence is exact at the position Z/2Z

Special cases

To make sense of the definition, it is helpful to consider what it means in relatively simple cases where the sequence is finite and begins or ends with 0.

• The sequence 0 → A → B is exact at A if and only if the map from A to B has kernel {0}, i.e. if and only if that map is a monomorphism.
• Dually, the sequence B → C → 0 is exact at C if and only if the image of the map from B to C is all of C, i.e. if and only if that map is an epimorphism.
• A consequence of these last two facts is that the sequence 0 → X → Y → 0 is exact if and only if the map from X to Y is an isomorphism.

When dealing with exact sequences of groups, it is common to write 1 instead of 0 for the trivial group with a single element.

Important are short exact sequences, which are exact sequences of the form

By the above, we know that for any such short exact sequence, f is a monomorphism and g is an epimorphism. Furthermore, the image of f is equal to the kernel of g. It is helpful to think of A as a subobject of B with f being the embedding of A into B, and of C as the corresponding factor object B/A, with the map g being the natural projection from B to B/A (whose kernel is exactly A).

Facts

The splitting lemma states that if the above short exact sequence admits a morphism t: B → A such that t o f is the identity on A or a morphism u: C → B such that g o u is the identity on C, then B is a twisted direct sum of A and C. (For groups, a twisted direct sum is a semidirect product; in an Abelian category, every twisted direct sum is an ordinary direct sum.) In this case, we say that the short exact sequence splits.

The snake lemma shows how a commutative diagram with two exact rows gives rise to a longer exact sequence. The nine lemma is a special case.

The five lemma gives conditions under which the middle map in a commutative diagram with exact rows of length 5 is an isomorphism; the short five lemma is a special case thereof applying to short exact sequences.

The importance of short exact sequences is underlined by the fact that every exact sequence results from "weaving together" several overlapping short exact sequences. Consider for instance the exact sequence

<math>A_1\to A_2\to A_3\to A_4\to A_5\to A_6<math>

and define

<math>C_k = \ker (A_k\to A_{k+1})= \operatorname{im} (A_{k-1}\to A_k) = \operatorname{coker} (A_{k-2}\to A_{k-1})<math>

Then we obtain a commutative diagram in which all the diagonals are short exact sequences:

Missing image
Long_short_exact_sequences.png
image:long_short_exact_sequences.png

Conversely, given any list of overlapping short exact sequences, their middle terms form an exact sequence in the same manner.

Applications of exact sequences

In the theory of abelian categories, short exact sequences are often used as a convenient language to talk about sub- and factor objects.

The extension problem is essentially the question, given the end terms A and C of a short exact sequence, what possibilities exist for the middle term B? In the category of abelian groups, this is equivalent to the question, what groups B have A as a normal subgroup and C as the corresponding factor group? This problem is important in the classification of groups.

Notice that in an exact sequence, the composition f_i+1 o f_i maps A_i to 0 in A_i+2, so every exact sequence is a chain complex. Furthermore, only f_i-images of elements of A_i are mapped to 0 by f_i+1, so the homology of this chain complex is trivial. More succinctly:

Exact sequences are precisely those chain complexes which are acyclic.

Given any chain complex, its homology can therefore be thought of as a measure of the degree to which it fails to be exact.

If we take a series of short exact sequences linked by chain complexes (that is, a short exact sequence of chain complexes, or from another point of view, a chain complex of short exact sequences), then we can derive from this a long exact sequence (i.e. an exact sequence indexed by the natural numbers) by repeated application of the snake lemma. This is explained in the article on homology. It comes up in algebraic topology in the study of relative homology; the Mayer-Vietoris sequence is another example. Long exact sequences induced by short exact sequences are also characteristic of derived functors.

Exact functors are functors that transform exact sequences into exact sequences.de:Exakte Folge