Soap bubble

A soap bubble is a very thin film of soap water that forms a hollow spherical shape with an iridescent surface. Soap bubbles usually last for only a few moments and burst either on their own or on contact with another object. Due to their fragile nature they have also become a metaphor for something that is attractive, yet insubstantial. They are mostly used as a children's plaything, but their usage in artistic performances shows that they can be fascinating for adults too. Soap bubbles can help to solve complex mathematical problems of space, as they will always find the smallest surface area between points or edges.

Physics

Surface tension and shape

Soap bubbles can exist because the surface layer of a liquid—in this case water—has a certain surface tension, which causes the layer to behave as an elastic sheet. A common misconception is that soap increases the water's surface tension. Actually soap does the exact opposite, decreasing it to approximately one third the surface tension of pure water. Soap does not strengthen bubbles, it stabilizes them, via an action known as the Marangoni effect. As the soap film stretches, the concentration of soap decreases, which causes the surface tension to increase. Thus, soap selectively strengthens the weakest parts of the bubble and tends to prevent them from stretching further. In addition, the soap reduces evaporation so the bubbles last longer.

Their spherical shape is also caused by surface tension. The tension causes the bubble to form a sphere, as a sphere has the smallest possible surface area for a given volume. This shape can be visibly distorted by air currents, and hence by blowing. If a bubble is left to sink in still air, however, it remains very nearly spherical, more so for example than the typical cartoon depiction of a raindrop. When a sinking body has reached its terminal velocity, the drag force acting on it is equal to its weight, and since a bubble's weight is much smaller in relation to its size than a raindrop's, its shape is distorted much less. (The surface tension opposing the distortion is similar in the two cases: The soap reduces the water's surface tension to approximately one third, but it is effectively doubled since the film has an inner and an outer surface.)

Freezing

Soap bubbles blown into air that is below a temperature of around 0° Fahrenheit (–15° Celsius) will freeze when they touch a surface. The air inside will gradually diffuse out, causing the bubble to crumple under its own weight. At temperatures below approximately –15° Fahrenheit (–25° Celsius), the bubbles will freeze in the air and shatter when they hit the ground.

Merging

Missing image
Soap_Bubble_-_foliage_background_-_iridescent_colours_-_Traquair_040801.jpg

Soap bubbles can easily merge

A graphic of merging soap bubbles

Missing image
Soapbubbles1b.jpg

Bubbles in a washing-up bowl

In the diagram above a ray of light hits the surface at point X. Some of the light is reflected, but some travels through the bubble wall and is reflected at the other side

In this diagram we look at two rays of red light (rays 1 and 2). Both rays are split as before and follow two possible paths, but we are interested only in the paths that are represented by the solid lines. Consider the ray emerging at Y. It consists of two rays on top of one another: the bit that went through the bubble wall for ray 1 and the bit that was reflected off the outer wall of ray 2. Ray one has travelled XOY further than ray 2. Since XOY happens to correspond to the wavelength of red light, the two rays are in phase (the humps and troughs are together).

This is similar to the diagram above except the wavelength is different. This time XOY is not a number of whole wavelengths and so ray 1 and 2 arrive at y out of step. The troughs of ray 1 line up with the humps of ray 2 and the two rays cancel each other out. The overall effect is that no blue light will be reflected for this thickness of bubble.

Missing image
Colours_reflected_from_a_thin_water_film_depending_on_thickness_and_angle_of_incidence.png

This computed image shows the colours reflected by a thin film of water illuminated by unpolarized white light. The radius is proportional to the thickness of the film, and the polar angle is the angle of incidence.

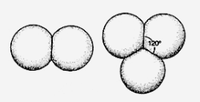
When two bubbles merge, the same physical principles apply, and the bubbles will adopt the shape with the smallest possible surface area. Their common wall will bulge into the larger bubble, as smaller bubbles have a higher internal pressure. If the bubbles are of equal size, the wall will be flat.

At a point where two or more bubbles meet, they sort themselves out so that only three bubble walls meet along a line, separated by angles of 120°. This is the most efficient choice, again, which is also the reason why the cells of a beehive use the same 120° angle, thus forming hexagons. Only four bubble walls can meet at a point, with the lines where triplets of bubble walls meet separated by 109.47°.

Interference and reflection

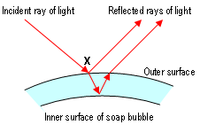
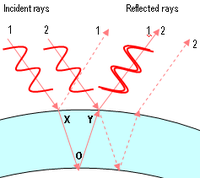
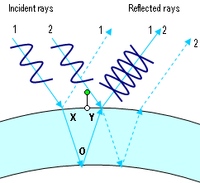
The iridescent colours of soap bubbles are caused by interfering light waves. As light impinges on the film, some of it is reflected off the outer surface while some of it enters the film and reemerges after being reflected back and forth between the two surfaces. The total reflection observed is determined by the interference of all these reflections. Since each traversal of the film incurs a phase shift proportional to the thickness of the film and inversely proportional to the wavelength, the result of the interference depends on these two quantities. Thus, at a given thickness, interference is constructive for some wavelengths and destructive for others, so that white light impinging on the film is reflected with a hue that changes with thickness.

A change in colour can be observed while the bubble is thinning due to evaporation. Thicker walls cancel out red (longer) wavelengths, thus causing a blue-green reflection. Later, thinner walls will cancel out yellow (leaving blue light), then green (leaving magenta), then blue (leaving yellow). Finally, when the bubble's wall becomes much thinner than the wavelength of visible light, all the waves in the visible region cancel each other out and no reflection is visible at all. When this state is observed, the wall is thinner than about one millionth of an inch (25 nanometres)—and is probably about to pop.

Interference effects also depend upon the angle at which the light strikes the film, an effect called iridescence. So, even if the wall of the bubble were of uniform thickness, one would still see variations of color due to curvature and/or movement. However, the thickness of the wall is continuously changing as gravity pulls the liquid downwards, so bands of colours that move downwards can usually also be observed.

Mathematical properties

Soap bubbles are also physical illustrations of the problem of minimal surfaces, an area of intense mathematical and scientific study over the past 15 years. For example, while it has been known since 1884 that a spherical soap bubble is the least-area way of enclosing a given volume of air (a theorem by Schwarz), it was only recently proved in the year 2000 that two merged soap bubbles provide the optimum way of enclosing two given volumes of air with the least surface area. This has been termed the double bubble theorem.

How to make soap bubbles

The easiest ways are to use commercially produced soap bubble fluid (marketed as a toy) or to simply put some dish washing soap in water. However, this latter might not work as well as expected, and there are several tricks to improve the soap sud formula:

Additives

• Something to reduce the water's surface tension: Liquid soap or baby shampoo. These may work better the more pure (devoid of perfume or other additives) the soap is, or perhaps with more expensive soaps.
• Something to thicken the water. Most commonly used is glycerin (available at the pharmacy), which makes the bubbles more colourful, too. Sugar, icing sugar or corn syrup have similar effects. It may be advantageous to dissolve the sugar in hot water. However, the soap sud can also be too thick and heavy, so it is important not to add too much of these thickening substances.
• Distilled water. As tap water contains calcium ions, and these bind the soap, distilled water works better.

Procedure

• Leaving the soap sud in an open container overnight makes it thicker, too. But again, if the solution becomes too heavy it will be harder to make soap bubbles.
• Bubbles or foam on the surface of the soap sud should be avoided by stirring gently, skimming them away or simply waiting until they are gone.
• How easy it is to make soap bubbles depends on a vast number of factors. Every soap is different, and environmental conditions influence performance, too. For example, dusty air is unfavourable, and so is wind. Also, the more humid the air is, the better, which means making soap bubbles is easier on rainy days. Altogether, the best procedure for finding the perfect solution is the trial and error method.

Bubble blowers

The easiest way is to use one of the plastic blowers that are sold with most commercial soap bubble solutions. However, as the blower's diameter determines the size of the soap bubble it might be necessary to build a blower oneself.

Generally, any closed ring structure works. A blower can be made by bending a wire a into loop with a handle, where the wire should be thick enough so the ring remains stiff. It can be improved by wrapping a thread or bandages around the wire so the soap water can stick better to the ring.

A "giant bubble" blower, using a cloth loop attached to a plastic wand, with a slide permitting the loop to be gently opened or closed, was popularized by Klutz Press Publishing, which published a bubble-blowing book with the blower attached.

Also, bubbles can be blown by using a bubble pipe, which is made of plastic and usually takes the shape of a smoking pipe, but sometimes has multiple bowls instead of just one. The bubble solution is poured into the bowl of the pipe, and then the person puts the mouthpiece in his or her mouth and blows. Bubbles then rise from the bowl.

Sample formulae

1. General purpose formula:
   • ²/₃ cup dish washing detergent
   • 1 gallon water
   • 2 to 3 tablespoons of glycerin
2. Another general purpose formula:
   • 100 g sugar
   • 2–3 tablespoons salt
   • 1.4 l water, better distilled water
   • 150 ml dish washing detergent
   • 12 ml glycerin
3. Yet another general purpose formula:
   • 1 part of washing-up detergent
   • 2 parts of glycerin
   • 3 parts of water
4. For long living bubbles:
   • ¹/₃ cup commercial bubble solution
   • ¹/₃ cup water
   • ¹/₃ cup glycerin
5. For no-tears soap bubbles:
   • 60 ml baby shampoo
   • 200 ml water
   • 3 tablespoons corn syrup

Performance art

Soap bubble performances combine entertainment with artistic achievement. They require a high degree of skill as well as perfect bubble suds. Some artists create giant bubbles or tubes, often enveloping objects or even humans. Others manage to create bubbles forming cubes, tetrahedra and other shapes or sculptures. Bubbles are often handled with bare hands. To add to the visual experience, they are sometimes filled with smoke or helium and combined with laser lights or fire. Soap bubbles can be filled with a flammable gas such as natural gas and then ignited. Of course this destroys the bubble.

See also

Joseph Plateau, formulator of Plateau's laws on the geometry of intersecting soap films, and Plateau's problem.

References

• A more detailed scientific explanation (http://www.exploratorium.edu/ronh/bubbles/bubbles.html)
• The proof paper on the Double Bubble Theorem (http://www.ugr.es/~ritore/bubble/bubble.htm)
• A book about soap bubbles and mathematics:
  Oprea, John (2000). The Mathematics of Soap Films—Explorations with Maple. American Mathematical Society (1st ed.). ISBN 0-82-182118-0
• Boys, C. V. (1890) Soap-Bubbles and the Forces that Mould Them; (Dover reprint) ISBN 0-48-620542-8. Classic Victorian exposition, based on a series of lectures originally delivered "before a juvenile audience."
• Isenberg, Cyril (1992) The Science of Soap Films and Soap Bubbles ; (Dover) ISBN 0486269604.fr:Bulle de savon

de:Seifenblase ja:シャボン玉 simple:Soap bubble