Snub cube
|
|
| Snub cube | |
|---|---|
 Click on picture for large version. Click here for spinning version. | |
 Click on picture for large version. Click here for spinning version. | |
| Type | Archimedean |
| Faces | 32 triangles 6 squares |
| Edges | 60 |
| Vertices | 24 |
| Vertex configuration | 3,3,3,3,4 |
| Symmetry group | octahedral (O) |
| Dual polyhedron | pentagonal icositetrahedron |
| Properties | convex, semi-regular (vertex-uniform), chiral |
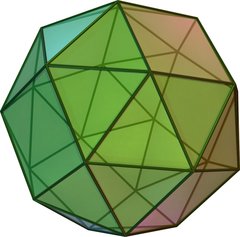
The snub cube, or snub cuboctahedron, is an Archimedean solid, usually regarded as a truncated polyhedron derived by truncating either a cube or an octahedron.
Missing image
Snub_cube_flat.png
image:Snub cube flat.png
The snub cube has 38 faces, of which 6 are squares and the other 32 are equilateral triangles. It has 60 edges and 24 vertices. In three-dimensional space, it has two distinct forms, which are mirror images (or "enantiomorphs") of each other. In higher-dimensional spaces, these are congruent.
Canonical coordinates for a snub cube are all the even permutations of (±1, ±ξ, ±1/ξ) with an even number of plus signs, along with all the odd permutations with an odd number of plus signs, where ξ is the real solution to ξ3+ξ2+ξ=1, which can be written
- <math>\xi = \frac{1}{3}\left(\sqrt[3]{17+\sqrt{297}} - \sqrt[3]{-17+\sqrt{297}} - 1\right)<math>
or approximately 0.543689. Taking the even permutations with an odd number of plus signs, and the odd permutations with an even number of plus signs gives a different snub cube, the mirror image.
The snub cube should not be confused with the truncated cube.
See also
External links
- The Uniform Polyhedra (http://www.mathconsult.ch/showroom/unipoly/)
- Virtual Reality Polyhedra (http://www.georgehart.com/virtual-polyhedra/vp.html) The Encyclopedia of Polyhedra
