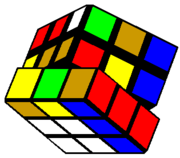
Rubik's Cube
|
|
Rubik_float.png
Rubik's Cube is a mechanical puzzle invented by the Hungarian sculptor and professor of architecture Ernő Rubik in 1974. It has been estimated that over 100,000,000 Rubik's Cubes or imitations have been sold worldwide.
| Contents |
History
The Rubik's Cube reached its height of popularity during the early 1980s, and it is still a popular toy nowadays. Many similar puzzles were released shortly after the Rubik's Cube, both from Rubik himself and from other sources, including the Rubik's Revenge, a 4 × 4 × 4 version of the Rubik's Cube. There are also 2 × 2 × 2 and 5 × 5 × 5 cubes (known as the Pocket Cube and the Professor's Cube, respectively), and puzzles in other shapes, such as the Pyraminx, a tetrahedron.
"Rubik's Cube" is a trademark of Seven Towns Limited. Ernő Rubik holds Hungarian patent HU170062 for the mechanism, but did not take out international patents. Ideal Toys was somewhat reluctant to produce the toy for that reason, and indeed clones appeared almost immediately. Ideal Toys later lost, in 1984, a patent infringement suit by Larry Nichols for his patent US3655201. [1] (http://patft.uspto.gov/netacgi/nph-Parser?Sect1=PTO1&Sect2=HITOFF&d=PALL&p=1&u=/netahtml/srchnum.htm&r=1&f=G&l=50&s1=3655201.WKU.&OS=PN/3655201&RS=PN/3655201) Terutoshi Ishigi acquired Japanese patent JP55‒8192 for a nearly identical mechanism while Rubik's patent was being processed, but Ishigi is generally credited with an independent reinvention. [2] (http://cubeman.vg-network.com/cchrono.txt)[3] (http://dev.rubiks.com/lvl3/index_lvl3.cfm?lan=eng&lvl1=inform&lvl2=medrel&lvl3=medvlt&lvl4=result)[4] (http://inventors.about.com/library/weekly/aa040497.htm)
Description
A Rubik's Cube is a plastic cube with its surface subdivided so that each face consists of nine squares. Each face can be rotated, giving the appearance of an entire slice of the block rotating upon itself. This gives the impression that the cube is made up of 27 smaller cubes (3 × 3 × 3). In its original state each side of the Rubik's Cube is a different color, but the rotation of each face allows the smaller cubes to be rearranged in many different ways.
The challenge is to return the Cube from any state to its original state, in which each face consists of nine squares of a single colour.
Workings
A standard cube measures approximately 2 1/8 inches (5.4 cm) on each side. The puzzle consists of the 26 unique miniature cubes ("cubies") on the surface. However, the centre cube of each face is merely a single square facade; all are affixed to the core mechanisms. These provide structure for the other pieces to fit into and rotate around. So there are 21 pieces: a single core, of three intersecting axes holding the six centre squares in place but letting them rotate, and 20 smaller plastic pieces which fit into it to form a cube. The cube can be taken apart without much difficulty, typically by prying an "edge cubie" away from a "center cubie" until it dislodges. It is a simple process to "solve" a cube in this manner, by reassembling the cube in a solved state; however, this is not the challenge.
There are 12 edge pieces which show two colored sides each, and 8 corner pieces which show three colours. Each piece shows a unique colour combination, but not all combinations are realized (For example, there is no edge piece showing both white and yellow, if white and yellow are on opposite sides of the solved cube). The location of these cubes relative to one another can be altered by twisting an outer third of the cube 90 degrees, 180 degrees or 270 degrees; but the location of the coloured sides relative to one another in the completed state of the puzzle cannot be altered: it is fixed by the relative positions of the centre squares and the distribution of colour combinations on edge and corner pieces. For most recent Cubes, the colors of the stickers are red opposite orange, yellow opposite white, and green opposite blue. However, there also exist Cubes with alternative color arrangements. These alternative Cubes have the yellow face opposite the green, and the blue face opposite the white (with red and orange opposite faces remaining unchanged).
Solutions
Many general solutions for the Rubik's Cube have been discovered independently (see How to solve the Rubik's Cube for one such solution). A popular method is "layer by layer", in which one face is solved, followed by the middle row, and finally the last and bottom face. The fastest methods, used by world champions, are "corners first" methods, or combinations of several other methods.
Solutions typically consist of a sequence of processes. A process is a series of cube twists which accomplishes a particular goal. For instance, one process might switch the locations of three corner pieces, while leaving the rest of the pieces in their places. These sequences are performed in the appropriate order to solve the cube. Complete solutions can be found in any of the books listed in the bibliography, and most can be used to solve any cube in under five minutes. In addition, much research has been done on Optimal solutions for Rubik's Cube.
Patrick Bossert, a 12 year old schoolboy from Britain, published his own solution in a book called You Can Do the Cube (ISBN 0140314830). The book sold over 1.5 million copies worldwide in 17 editions and became the number one book on both The Times and the New York Times bestseller lists for 1981.
A Rubik's Cube can have (8! × 38−1) × (12! × 212−1)/2 = 43,252,003,274,489,856,000 different positions (~4.3 × 1019), about 43 quintillion, but it is advertised only as having "billions" of positions, due to the general incomprehensibility of that number. Despite the vast number of positions, all cubes can be solved in 29 moves or fewer.
Competitions
Many speedcubing competitions have been held to determine who can solve the Rubik's Cube in the shortest amount of time. The first world championship was held on 5 June 1982 in Budapest and was won by Minh Thai, a Vietnamese student from Los Angeles with a time of 22.95 seconds. The official world record of 14.52 seconds (average of 5 cubes) was set on October 16th 2004 in Pasadena by Shotaro "Macky" Makisumi, a Japanese high school student living in California. This record is recognized by the World Cube Association, the official governing body which regulates events and records. Makisumi was an 8th grade student at the time at the age of 14 participating in the Caltech 2004 Fall Tournament.
Many individuals have recorded shorter times, but these records were not recognized due to lack of compliance with agreed-upon standards for timing and competing. Therefore only records set during official World Cube Association sanctioned tournaments are acknowledged.
In 2004, the World Cube Association established a new set of standards, with a special timing device called a Stackmat timer. The World Cube Association consists of board members Ron van Bruchem of The Netherlands, Tyson Mao of the United States, a Gilles Roux of France.
Rubik's Cube as a mathematical group
Many mathematicians are interested in the Rubik's Cube partly because it is a tangible representation of a mathematical group. Specifically, the cube group is the set of all legal cube operations with composition as the group operation.
The order of the cube group is equal to the number of possible positions obtainable by the cube. This is:
- <math>\frac{1}{12}8!\,3^8 12!\,2^{12}<math>
or 43,252,003,274,489,856,000. This factorizes as
- 2273145372111.
Because of the large size of the cube group it is sometimes useful to analyze the structure with the assistance of a computer algebra system such as GAP (see [5] (http://www.gap-system.org/Doc/Examples/rubik.html)).
Let Cube be the group of all legal cube operations. In the following, we assume the notation described in How to solve the Rubik's Cube. Also we assume the orientation of the six centre pieces to be fixed.
We consider two subgroups of Cube: First the group of cube orientations, Co, which leaves every block fixed, but can change its orientation. This group is a normal subgroup of the Cube group. It can be represented as the normal closure of some operations that flip a few edges or twist a few corners. For example the normal closure of the following two operation is Co BR'D2RB'U2BR'D2RB'U2, (twist two corners) RUDB2U2B'UBUB2D'R'U'. (flip two edges)
For the second group we take Cube permutations, Cp, which can move the blocks around, but leaves the orientation fixed. For this subgroup there are more choices, depending on the precise way you fix the orientation. One choice is the following group, given by generators: (The last generator is a 3 cycle on the edges).
Cp = [U2, D2, F, B, L2, R2, R2U'FB'R2F'BU'R2 ]
Since Co is a normal subgroup, the intersection of Cube orientation and Cube permutation is the identity, and their product is the whole cube group, it follows that the cube group is the semidirect product of these two groups. That is
Next we can take a closer look at these two groups. Co is an abelian group, it is <math>\mathbb Z_3^7 \times \mathbb Z_2^{11}<math>.
Cube permutations, Cp, is little more complicated. It has the following two normal subgroups, the group of even permutations on the corners <math>A_8<math> and the group of even permutations on the edges <math>A_{12}<math>. Complementary to these two groups we can take a permutation that swaps two corners and swaps two edges. We obtain that
Putting all the pieces together we get that the cube group is isomorphic to
- <math>(\mathbb Z_3^7 \times \mathbb Z_2^{11})<math>
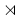 <math>\,((A_8 \times A_{12})<math>
<math>\,((A_8 \times A_{12})<math> 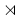 <math>\mathbb Z_2)<math>.
<math>\mathbb Z_2)<math>.
This group can also be described as the quotient group
[(Z37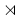 S8)×(Z211
S8)×(Z211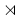 S12)]/Z2. When one wants to take
the possible permutations of the centre pieces into account, an other direct component arises, which describes the 24 rotations of cube as a whole
, if call this group T, we obtain: T×[(Z37
S12)]/Z2. When one wants to take
the possible permutations of the centre pieces into account, an other direct component arises, which describes the 24 rotations of cube as a whole
, if call this group T, we obtain: T×[(Z37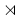 S8)×(Z211
S8)×(Z211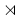 S12)]/Z2.
S12)]/Z2.
The simple groups that occur as quotients in the composition series of R' are <math>A_8,A_{12},\mathbb{Z}_3\ (7\ \mbox{times}),\mathbb{Z}_2\ (12\ \mbox{times})<math>.
Parallel with particle physics
A parallel between Rubik's Cube and particle physics was noted by mathematician Solomon W. Golomb, and then extended (and modified) by Anthony E. Durham. Essentially, clockwise and counterclockwise "twists" of corner cubies may be compared to the electric charges of quarks (+2/3 and −1/3) and antiquarks (−2/3 and +1/3). Feasible combinations of cubie twists are paralleled by allowable combinations of quarks and antiquarks—both cubie twist and the quark/antiquark charge must total to an integer. Combinations of two or three twisted corners may be compared to various hadrons. This, however, is not always feasible.
A greater challenge
Most Rubik's Cubes are sold without any markings on the center faces. This obscures the fact that the center faces can rotate independently. If you have a marker pen, you could, for example, mark the central squares of an unshuffled cube with four colored marks on each edge, each corresponding to the color of the adjacent square. Some cubes have also been commercially produced with markings on all of the squares, such as the Lo Shu magic square or playing card suits. You might be surprised to find you could scramble and then unscramble the cube but still leave the markings rotated.
Putting markings on the Rubik's cube increases the challenge of solving the cube, chiefly because it expands the set of distinct possible configurations. It can be shown that, when the cube is unscrambled apart from the orientations of the central squares, there will always be an even number of squares requiring a quarter turn.
See also
References
- Handbook of Cubik Math by Alexander H. Frey, Jr. and David Singmaster
- Notes on Rubik's 'Magic Cube' ISBN 0-89490-043-9 by David Singmaster
- Metamagical Themas by Douglas R. Hofstadter contains two insightful chapters regarding Rubik's Cube and similar puzzles, originally published as articles in the March 1981 and July 1982 issues of Scientific American.
- Four-Axis Puzzles by Anthony E. Durham.
- Mathematics of the Rubik's Cube Design ISBN 0-80593-919-9 by Hana M. Bizek
External links
- Patents
- BE887875 (http://v3.espacenet.com/textdoc?IDX=BE887875&QPN=BE887875) -- "Rubik's Cube " -- Ernö Rubik -- July 1, 1981
- Joshua Bell, "Magic Polyhedra Patents (http://www.calormen.com/TwistyPuzzles/twisty.htm)". August 27, 2004.
- Rubik's Cube and its variants:
- Rubik's Cube Art:
- Solutions for the puzzle:
- http://jeays.net/rubiks.htm
- http://cube.helm.lu
- http://lar5.com/cube/index.html
- Beginner Solution to the Rubik's Cube (http://www.geocities.com/jasmine_ellen/RubiksCubeSolution.html)
- http://www.nerdparadise.com/puzzles/333
- Simple Way of Solving the Rubik's Cube (http://www.geocities.com/cub3r_alan@sbcglobal.net/solution.html)
- Official world records:
- Unofficial world records:
- World championship 2003:
- European championship 2004:
- Online versions of Rubik's Cube:
- Rubik's Cube Java Applet: http://www.schubart.net/rc/
- Another Cube applet: http://user.tninet.se/~ecf599g/aardasnails/java/PuzzleApplet/webpages
- Yet Another Cube applet (with a more 3D feel): http://www.andkon.com/arcade/puzzle/rubikscube/
- An ActiveX version of this puzzle (play it and learn how to solve it): http://www.carobit.com/rubik/rubik.html
- Disassembled Cube (can be taken apart to see how the cube works): http://www.randelshofer.ch/rubik/virtualcubes/
- A JavaScript version to play online: http://en.ludanto.org/rubik.shtml
- The version 2x2x2 with JavaScript: http://en.ludanto.org/rubik2.shtml
- Magic Cube 4D (http://www.superliminal.com/cube/cube.htm) - 4D variantde:Rubiks Würfel
es:Cubo de Rubik fr:Cube de Rubik he:הקובייה ההונגרית it:Cubo di Rubik nl:Rubiks kubus ja:ルービックキューブ pl:Kostka Rubika fi:Rubikin kuutio sv:Rubiks kub zh:魔方