Robinson projection
|
|
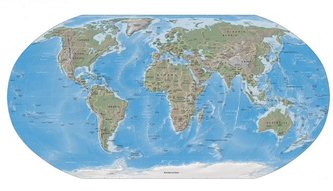
The Robinson projection is a map projection used for geographic maps.
Presented by Dr. Arthur H. Robinson in 1963, it is classified as a pseudo-cylindrical projection by reason of its straight parallels, each along which the meridians are spaced evenly. The central meridian is also a straight line; other meridians are curved. Robinson specified the projection to be constructed by referring to a table of cartesian coordinate values at specific intersections of latitude and longitude. Intermediate locations are to be found by interpolation. This method reflects the way he developed the projection as a series of trials, iterating until he settled on the meridian shapes and parallel spacing most pleasing to him. To contrast, most other projections are formulated as mathematical equations. Several formulaic representations of Robinson's projection have appeared in the literature as alternatives to the look-up tables.
Robinson developed the projection under commission from Rand McNally, which used it thenceforth in many atlases and books. It briefly carried the name "orthophanic" (meaning correct-looking) but quickly became known as the Robinson projection. National Geographic Society adopted it for their world maps in 1988 but abandoned it ten years later for the Winkel Tripel. Many educational institutes and textbooks followed National Geographic's example in adopting the projection, and most of those still use it.
Usgs_map_robinson.PNG
Like many projections, the Robinson has advantages. Like all projections, it also has disadvantages. The projection is neither equal-area nor conformal, abandoning both for a compromise the creator felt produces a better overall view than could be achieved by adhering to either. The meridians curve gently, avoiding extremes, but thereby stretch the poles into long lines instead of leaving them as points. Hence distortion close to the poles is severe but quickly declines to moderate levels moving away from them. The straight parallels imply severe angular disortion at the high latitutes toward the outer edges of the map, a fault inherent in any pseudocylindrical projection.
See also
- Cartography
- Gall-Peters projection
- Mercator projection
- Nautical chart
- Oblique Mercator projection
- Transverse Mercator projection
References
- John B. Garver Jr., "New Perspective on the World", National Geographic, December 1988, pp. 911-913.
- John P. Snyder, Flattening The Earth - 2000 Years of Map Projections, The University of Chicago Press, 1993, pp. 214-216.
