Quasinormal mode
|
|
General Definition
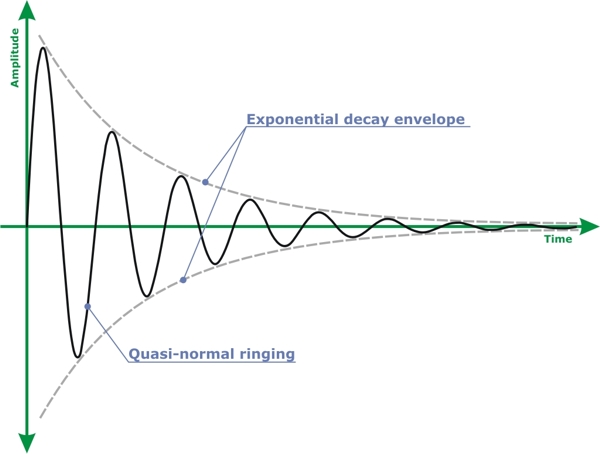
Quasinormal modes (QNM) are the modes of energy dissipation of a perturbed object or a field. Consider a familiar example where one perturbs (gently hits) a wine glass with a knife: the glass begins to ring, it rings with a set, superposition if you will, of its natural frequencies -- its modes of sonic energy dissipation. One might be tempted to call those modes normal, however the glass does not go on ringing forever, amplitude of oscillation decays in time; we therefore call its modes quasi-normal. To a very high degree of accuracy, quasinormal ringing can be approximated by
- <math>\psi(t) \approx e^{-\omega^{\prime\prime}t}\cos\omega^{\prime}t<math>
where <math>\psi\left(t\right)<math> is the amplitude of oscillation, <math>\omega^{\prime}<math> is the frequency, and <math>\omega^{\prime\prime}<math> is the decay rate. Quasinormal mode, two numebrs, is
- <math>\omega = \left(\omega^{\prime} , \omega^{\prime\prime}\right)<math>
or, more compactly
- <math>\psi\left(t\right) \approx e^{i\omega t}<math>
- <math>\omega =\omega^{\prime} + i\omega^{\prime\prime}<math>
where <math>\psi\left(t\right)<math> stands for the real part. Here, <math>\mathbf{\omega}<math> is what is commonly referred to as the quasinormal mode. It is a complex number with two pieces of information: real part is the temporal oscillation; imaginary part is the temporal, exponential decay.
In certain cases the amplitude of the wave decays quickly, to follow the decay for a longer time one may plot <math>\log\left|\psi(t)\right|<math>
- Missing image
Log(abs(qnm)).jpg
Image:log(abs(qnm)).jpg
- Missing image
I'll be back...
Someone else wrote something really confusing...
In theoretical physics, a quasinormal mode is a formal solution of linearized differential equations (such as the linearized equations of general relativity constraining perturbations around a black hole solution) with a complex eigenvalue (frequency).
Black holes have many quasinormal modes (also: ringing modes) that describe the exponential decrease of asymmetry of the black hole in time as it evolves towards the perfect spherical shape.
Recently, the properties of quasinormal modes have been tested in the context of the AdS/CFT correspondence. Also, the asymptotic behavior of quasinormal modes was proposed to be related to the Immirzi parameter in loop quantum gravity, but convincing arguments have not been found yet.