Nomogram
|
|
- This article is about the graphical devices called nomograms. For a description of the Japanese puzzles called nonograms see Paint by numbers.
A nomogram or nomograph is a graphical calculating device, a two-dimensional diagram designed to allow the approximate graphical computation of a function. Like a slide rule, it is a graphical analog computation device; and, like the slide rule, its accuracy is limited by the precision with which physical markings can be drawn, reproduced, viewed, and aligned. Most nomograms are used in applications where an approximate answer is appropriate and useful. Otherwise, the nomogram may be used to check an answer obtained from an exact calculation method.
The slide rule is intended to be a general-purpose device. Nomograms are usually designed to perform a specific calculation, with tables of values effectively built in to the construction of the scales.
A nomogram typically has three scales: two scales represent known values and one scale is the scale where the result is read off. The known scales are placed on the outside; i.e. the result scale is in the center. Each known value of the calculation is marked on the outer scales and a line is drawn between each mark. Where the line and the inside scale intersects is the result. The scale marks include 'tick marks' to indicate exact number locations, and labeled reference values. These scales may be linear, logarithmic or have some more complex relationship. Straight scales are useful for relatively simple calculations, but for more complex calculations, simple or elaborate curved scales may need to be used.
Usage is simple — a taut string or other straight edge is placed so as to contact the two known values on their lines. The required answer is read off another line. This allows calculation of one variable when the other two are known. Additional lines are sometimes added that are simple conversions of one of the other variables.
One common nomogram that defies the above definition is a temperature graph. On this graph, degrees Fahrenheit and degrees Celsius are both indicated. While it is drawn as a single line with two scales, the two different scale markings indicate that there are actually two lines overlapping each other.
Examples of nomograms:
- Spiral-shaped nomogram -- the Cornu spiral
- The Smith chart (see figure, right), used in electronics and systems analysis
- nonlinearly ruled graph paper - probability rule, semi-log rule or log-log rule, all intended to represent various non-linear functions as straight lines on a graph.
More examples
Parallel-resistance/thin-lens nomogram
The nomogram below performs the computation
- <math>\frac{1}{1/A + 1/B}<math>
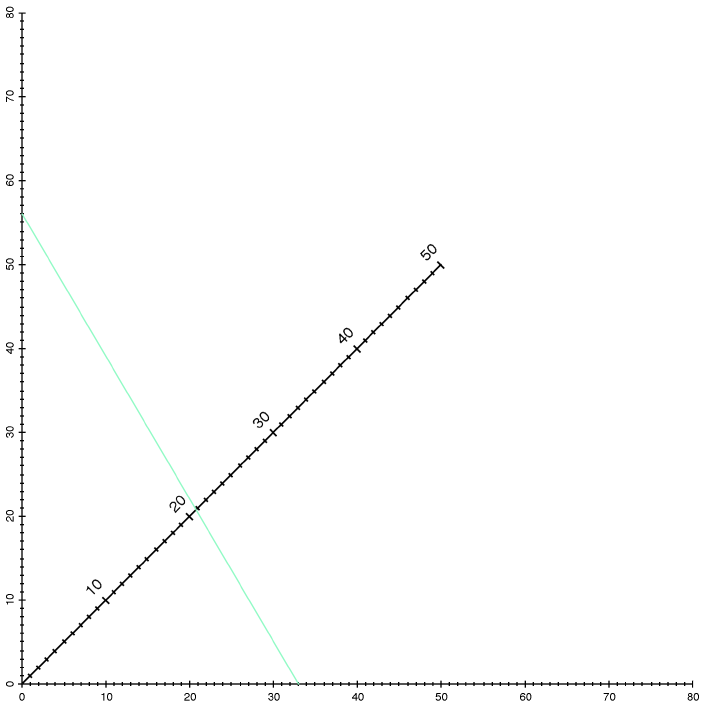
This nomogram is interesting because it performs a useful nonlinear calculation using only straight-line, equally-graduated scales.
A and B are entered on the horizontal and vertical scales, and the result is read from the diagonal scale. This formula has several uses: for example, it is the parallel-resistance formula in electronics, and the thin-lens equation in optics.
In the example below, the green line demonstrates that parallel resistors of 56 and 33 ohms have a combined resistance of about 21 ohms. It also demonstrates that an object at a distance of 56 cm from a lens whose focal length is 21 cm forms a real image at a distance of about 33 cm.
Chi-squared test computation nomogram
The nomogram below can be used to perform an approximate computation of some values needed when performing a familiar statistical test, Pearson's chi-square test. This nomogram demonstrates the use of curved scales with unevenly-spaced graduations.
The blue line demonstrates the computation of
- (9 − 5)2/ 5 = 3.2
The red line demonstrates the computation of
- (81 − 70)2 / 70 = 1.7
In performing the test, Yates' correction for continuity is often applied, and simply involves subtracting 0.5 from the observed values. A nomogram for performing the test with Yates' correction could be constructed simply by shifting each "observed" scale half a unit to the left, so that the 1.0, 2.0, 3.0, ... graduations are placed where the values 0.5, 1.5, 2.5, ... appear on the present chart.
Missing image
Chisquarenomo3.png
image:chisquarenomo3.png