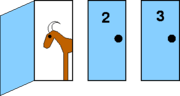
Monty Hall problem
|
|
The Monty Hall problem is a puzzle in probability that is loosely based on the American game show Let's Make a Deal; the name comes from the show's host Monty Hall. In this puzzle a player is shown three closed doors; behind one is a car, and behind each of the other two is a goat. The player is allowed to open one door, and will win whatever is behind the door. However, after the player selects a door but before opening it, the game host opens another door to reveal a goat. The host then offers the player an option to choose the other closed door. Does switching improve the player's chance of winning the car? With the assumptions explicitly stated below, the answer is yes — switching results in a 2/3 chance of winning the car.
The problem is also called the Monty Hall paradox, in the sense that the solution is counterintuitive, although the problem is not a logical self-contradiction. It has generated heated debate.
| Contents |
Problem and solution
The problem
Here is a famous statement of the problem, from a letter from Craig F. Whitaker to Marilyn vos Savant's column in Parade Magazine in 1990 (as quoted by Bohl, Liberatore, and Nydick):
Suppose you're on a game show, and you're given the choice of three doors: Behind one door is a car; behind the others, goats. You pick a door, say No. 1, and the host, who knows what's behind the doors, opens another door, say No. 3, which has a goat. He then says to you, "Do you want to pick door No. 2?" Is it to your advantage to switch your choice?
This is a restatement of the problem as given by Steve Selvin in a letter to the American Statistician (February, 1975). As stated, the problem is an extrapolation from the game show; Monty Hall did open a wrong door to build excitement, but did not allow players to change their choice. As Monty Hall wrote to Selvin:
And if you ever get on my show, the rules hold fast for you—no trading boxes after the selection.
—(letsmakeadeal.com) (http://www.letsmakeadeal.com/problem.htm)
Selvin's subsequent letter to the American Statistician (August, 1975) appears to be the first use of the term "Monty Hall problem".
An essentially identical problem appeared as the "three prisoners problem" in Martin Gardner's Mathematical Games column in 1959. Gardner's version makes the selection procedure explicit, avoiding the unstated assumptions in the version given here.
A complete statement of the problem:
- The player picks one of three doors. The contents are not revealed.
- The game host knows what is behind every door.
- The game host must open one of the remaining doors and must make the offer to switch.
- The game host will always pick a goat.
- If the player picks a goat, the game host picks the other goat.
- If the player picks the car, the game host picks either of the two goats.
- The player is asked whether to stay with their first choice, or switch to the one remaining door.
Do the player's odds increase by switching?
The solution
The solution to the problem is yes; the chance of winning the car is doubled when the player switches to another door rather than sticking with the original choice.
There are three possible scenarios, all with equal probability (1/3):
- The player picks goat number one. The game host picks goat number two. Switching will win the car.
- The player picks goat number two. The game host picks goat number one. Switching will win the car.
- The player picks the car. The game host picks either of the two goats. Switching will lose.
In the first two scenarios, the player wins by switching. The third scenario is the only one where the player wins by staying. Since two out of three scenarios win by switching, the odds of winning by switching are 2/3.
When the player chooses a door, there is a 1/3 chance of choosing the car; there is a 2/3 chance of not choosing the car. When the host opens a door to reveal a goat, there is still a probability of 2/3 that the player has not chosen the car; knowing where one of the goats is does not change the probability of the original decision. Therefore, if the player switches to the only remaining choice, there is now a probability of 2/3 that the player has chosen the door with the car.
The problem would be completely different if there was no initial choice, or if the game host picked a door to open at random, or if the game host were permitted to make the offer to switch more often (or only) depending on knowledge of the player's original choice. For example, if the game host always had two goats to choose from, and the player was only asked for a choice once a goat was revealed (with two doors remaining), the odds would be 1/2. In the original problem, it is because the player has a 2/3 chance of eliminating one of the goats that the game host's decision reveals the correct answer 2/3 of the time.
Aids to understanding
Venn diagram
The probability that the car is behind the remaining door can be calculated with the Venn diagrams below. Here, the player chooses door 3.
Missing image
Monty2.gif
Image:monty2.gif
Increasing the number of doors
It may be easier for the reader to appreciate the result by considering a hundred doors instead of just three. In this case there are 99 doors with goats behind them and 1 door with a prize. The player picks a door; 99% of the time, the player will pick a door with a goat. So, there is very little chance of choosing the right door! The game host then opens 98 of the other doors revealing 98 goats and offers the player the chance to switch to the other unopened door. On 99 out of 100 occasions the door the player can switch to will contain the prize as 99 out of 100 times the player first picked a door with a goat. At this point a rational player should always switch.
Probability that first choice is wrong
Another way of phrasing why the player should switch: by switching, the player is ensuring a win if the first choice was a goat. The probability of picking a goat was 2/3, so the player should switch.
Combining doors
Instead of one door being opened and thus eliminated from the game, it may equivalently be regarded as combining two doors into one, as a door containing a goat is essentially the same as a door with nothing behind it. In essence, this means the player has the choice of either sticking with their original choice of door, or choosing the sum of the contents of the two other doors. Clearly, the chance of the prize being in the other two doors is twice as high. Notice how the above assumptions play a role here: The reason switching is equivalent to taking the combined contents is that the game host is required to open a door with a goat.
Bayes' theorem
For the least reliance on verbiage and the most on formal mathematics, an approach using Bayes' theorem may be best. It also makes explicit the effect of the assumptions given earlier. Consider the position when door 1 has been chosen and no door has been opened. The probability that the car is behind door 2, p(C2), is plainly 1/3, as it may equally well be in any of the three places. The probability that the game host will open door 3, p(O3), is 1/2; if there can be any doubt, enumeration of cases will confirm this. But when the car is behind door 2, The game host will certainly open door 3, by the assumptions; that is, p(O3|C2) = 1. Hence the probability that the car is behind door 2 given that the game host opens door 3 is
- <math>
P(C2|O3) = \frac{P(O3|C2) P(C2)}{P(O3)}
= \frac{1 \times \frac{1}{3}}{\frac{1}{2}}
= \frac{2}{3}
<math>
Opposing player
Consider the game as a two-player game in which Player A chooses a door. The game host then opens a goat door. And Player B opens the remaining door. Since the first player will choose the car door only 1 in 3 times, the second player will win the car 2 out of 3 times. Thus, the car is behind the remaining door 2 out of 3 times.
Effect of opening a door
This analysis of the problem considers the player's options in terms of Staying or Switching, and the probabilities of each strategy paying off. Here's what the probabilities would be if the game host didn't open a door after the player's initial choice:
- Staying: The player can only win by Staying if the car happens to be behind the door the player first picked. Since there's a <math>\begin{matrix} \frac{1}{3} \end{matrix}<math> chance that the car is behind that door, the player's chance of winning by Staying is <math>\begin{matrix} \frac{1}{3} \end{matrix}<math>.
- Switching: The player can only win by Switching if the car isn't behind the door the player first picked, and if the player selects the correct door out of the two remaining when the player decides to switch. There is a <math>\begin{matrix} \frac{2}{3} \end{matrix}<math> chance that the car is behind one of those two doors, but only a <math>\begin{matrix} \frac{1}{2} \end{matrix}<math> chance that the player will select the correct one; since both these conditions must be met, the chance of winning by Switching is <math> \left ( \begin{matrix} \frac{2}{3} \end{matrix} \times \begin{matrix} \frac{1}{2} \end{matrix} \right ) <math>, or <math>\begin{matrix} \frac{1}{3} \end{matrix}<math>.
In this version, where the game host gives no additional information, the chances of winning by Staying or by Switching are the same. Here's what happens to the probabilities when the game host opens a door containing a goat (and thus eliminates an option):
- Staying: The player still can only win by Staying if the car happens to be behind the door the player first picked. Since there's still a <math>\begin{matrix} \frac{1}{3} \end{matrix}<math> chance that the car is behind that door, the player's chance of winning by Staying is still <math>\begin{matrix} \frac{1}{3} \end{matrix}<math>.
- Switching: The player still can only win by Switching is if the car isn't behind the door the player first picked. However, there are no longer two doors to pick from once the decision to switch is made; The game host has opened one of those two doors and eliminated it as a choice. The chance that the car was behind one of those two doors is now the chance that it is behind the only remaining one of those two doors, <math>\begin{matrix} \frac{2}{3} \end{matrix}<math>; now that the game host has eliminated the <math> \begin{matrix} \frac{1}{2} \end{matrix} <math> chance of guessing wrongly after deciding to switch, <math>\begin{matrix} \frac{2}{3} \end{matrix}<math> is the player's chance of winning by Switching.
Simulation
Instead of attempting to calculate the exact probability of winning the car, we can execute a simulation of the game and count the fraction of times the player wins. By the law of large numbers, this is likely to approximate the probability of winning. See empirical solution of the Monty Hall problem for Perl and Java programs that implement simulations. Here is the output of a sample run of the Perl program for the default 3000 iterations:
- Playing 3000 games...
- Grand totals:
- Sticker has won 1013 times
- Switcher has won 1987 times
Variants
With several minutes remaining in the game, the game host chose two players for the "Big Deal". Behind one of three doors was the grand prize. Each player was allowed to choose a door (not the same one).
In this scenario, a variant of Selvin's problem can be stated. The game host eliminates a player with a goat behind their door (if both players had a goat, one is eliminated at random, without letting the players know about it), opens the door and then offers the remaining player a chance to switch. Should the remaining player switch?
The answer is no. The reason: a switcher in this game will win if and only if both players originally pick goats. How likely is that? 1/3. A sticker will win in the remaining 2/3 of the cases. So stickers will win twice as often as switchers.
Alternatively, there are three possible scenarios, all with equal probability (1/3):
- Player 1 picks the door with the car. The host must eliminate player 2. Switching loses.
- Player 2 picks the door with the car. The host must eliminate player 1. Switching loses.
- Neither player picks the car. The host eliminates one of the players randomly. Switching wins.
Player 1 is the remaining player in the first case and half the time in the third case and switching loses (1/3 chance) twice as often as it wins (1/6 chance). Similarly, player 2 is the remaining player in the second case and half the time in the third, and loses twice as often by switching. Regardless of which player remains, there is 2/3 probability of winning with the sticking strategy.
There is a generalization of the original problem to n doors: in the first step, you choose a door. The game host then opens some other door that's a loser. If you want, you may then switch your allegiance to another door. The game host will then open an as yet unopened losing door, different from your current preference. Then you may switch again, and so on. This continues until there are only two unopened doors left: your current choice and another one. How many times should you switch, and when, if at all?
The best strategy is: stick with your first choice all the way through but then switch at the very end. With this strategy, the probability of winning is (n-1)/n. This was proved by Bapeswara Rao and Rao.
Origins
The game used in the Monty Hall problem is similar to three card monte, a gambling game in which the player has to find a single winning card among three face-down cards. As in the Monty Hall problem, the dealer knows where the winning card is, but here the dealer always tries to trick the player into picking the wrong card. As the card is often a Queen court card, it is also known as Find the Lady.
An older puzzle in probability theory involves three prisoners, one of whom (already chosen at random but unknown to the prisoners) is to be executed in the morning. The first prisoner begs the guard to tell him which of the other two will go free, arguing that this reveals no information about whether the prisoner will be the victim; the guard responds by claiming that if the prisoner knows that a specific one of the other two prisoners will go free it will raise the first prisoner's subjective chance of being executed from 1/3 to 1/2. The question is whether the analysis of the prisoner or the guard is correct. In the version given by Martin Gardner, the guard then performs a particular randomizing procedure for selecting which name to give the prisoner; this gives the equivalent of the Monty Hall problem without the usual ambiguities in its presentation.
Anecdotes
After this problem's solution was discussed in Marilyn vos Savant's "Ask Marilyn" question-and-answer column of Parade magazine in 1990, many readers including several mathematics professors wrote in to declare that her solution was wrong. An equally contentious discussion of Marilyn's discussion took place in Cecil Adams's column The Straight Dope.
The Monty Hall problem is discussed, from the perspective of a boy with autism, in The Curious Incident of the Dog in the Night-time, a 2003 novel by Mark Haddon.
References
- Bapeswara Rao, V. V. and Rao, M. Bhaskara (1992). "A three-door game show and some of its variants". The Mathematical Scientist 17, no. 2, pp. 89–94
- Bohl, Alan H.; Liberatore, Matthew J.; and Nydick, Robert L. (1995). "A Tale of Two Goats ... and a Car, or The Importance of Assumptions in Problem Solutions". Journal of Recreational Mathematics 1995, pp. 1–9.
- Gardner, Martin (1959). "Mathematical Games" column, Scientific American, October 1959, pp. 180–182.
- Selvin, Steve (1975a). "A problem in probability" (letter to the editor). American Statistician 29(1):67 (February 1975).
- Selvin, Steve (1975b). "On the Monty Hall problem" (letter to the editor). American Statistician 29(3):134 (August 1975).
- Tierney, John (1991). "Behind Monty Hall's Doors: Puzzle, Debate and Answer?", The New York Times July 21, 1991, Sunday, Section 1; Part 1; Page 1; Column 5
- vos Savant, Marilyn (1990). "Ask Marilyn" column, Parade Magazine p. 12 (Feb. 17, 1990). [cited in Bohl et al., 1995]
External links
- THE MONTY HALL PROBLEM (http://www.letsmakeadeal.com/problem.htm) (at letsmakeadeal.com; quotes Monty's letter to Steve Selvin in full)
- Monty Hall Paradox (let's make a deal) (http://www.mathematik.uni-bielefeld.de/~sillke/PUZZLES/monty-hall) (lengthy bibliography)
- Monty Hall Dilemma (http://www.cut-the-knot.org/hall.shtml) (Monty Hall simulation, discussions, and generalization)
- Grand Illusions (http://www.grand-illusions.com/monty.htm) Explanation and various simulatorsde:Ziegenproblem ja:モンティ・ホール問題