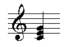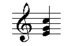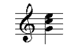Inversion (music)
|
|
- For non-musical meanings of inversion, see inversion.
In music theory, the word inversion has several meanings. There are inverted chords, inverted melodies, inverted intervals, and (in counterpoint) inverted voices. The concept of inversion also plays a role in musical set theory.
| Contents |
Inverted chords
An inverted chord is a chord which has a note other than its root note in the bass note. Since Rameau (1722), chords remain equivalent when inverted, being functions rather than sonorities. However, before Rameau factors including the regola delle terze e seste, "rule of sixths and thirds", which required the resolution of imperfect consonances to perfect ones, precluded the analysis of 64 sonorites as inversions of 53 sonorities.
For example, the root position of a triad of C major has the C in the bass:
A triad in root position, therefore, is made up of the root note and a third and a fifth above it. Triads in root position are also in normal form.
The first inversion of the same triad has the E, the third of the triad, in the bass:
This means that a triad in first inversion is made up of the root plus a third and a sixth above it. The second inversion has the fifth, the G, in the bass:
A triad in second inversion, therefore, is made up of the root plus a fourth and a sixth above it.
The third inversion of a triad does not really make much sense to discuss, since inverting the second inversion just leads to the tonic again, an octave higher. Chords of four notes or more, however, can be in their third inversion: the third inversion of a dominant seventh in C major, for example (made up of the notes G, B, D and F) has the seventh, F, in the bass. This gives a chord made up of the root plus a second, fourth and sixth above it.
The terms "root", "first inversion", and "second inversion" may also be applied to chords in which the notes are not closely spaced. For instance, C-G-E, where the E is a major sixth above G, is also considered to be in root position, and more generally, any C major chord in which C is the lowest note is considered to be in root position. Similarly, any C major chord with E on the bottom counts as a first inversion, any C major chord with G on the bottom counts as a second inversion; and analogously for all other chords.
Notations for inverted chords
There are at least four different notations for the inversions of chords.
(i) Perhaps the most commonly used method is figured bass. In this system, first inversions are normally indicated by the digit 6 and second inversions by the digits 64. A full presentation of figured bass notation is given in the Wikipedia article on this subject.
(ii) The letters a, b, c, etc., may be placed after any chord symbol to indicate the root, first and second inversion respectively. Hence the C chord below, in first inversion (i.e. with E in the bass) may be notated as Cb. (If no letter is added, the chord is assumed to be in root inversion, having the same meaning as if 'a' had been added explicitly.)
(iii) A less common, but occasionally used, notation for chord inversion is to place the number 1, 2 or 3 etc. after a chord to indicate that it is in first, second, or third inversion respectively. Hence the C chord above, in first inversion (i.e. with E in the bass) may be notated as C1. Note that no number is added in the case of a chord in root inversion. This notation should not be confused with a quite different meaning of the same notation, where a number is placed after a note name to indicate the octave in which a single note is to sound, e.g. C4 is often used simply to mean the single note middle C.
(iv) A notation for chord inversion often used in popular music is to write the name of a chord, followed by a forward slash, and then the name of the note that is to sound in the bass. For example, the C chord above, in first inversion (i.e. with E in the bass) may be notated as C/E. Interestingly, this notation works consistently even when a note not present in a triad or other chord is to sound in the bass, e.g. F/G is a way of notating a particular approach to voicing a G13th chord. This should not be confused with notations of the "function of function" style, for instance the subdominant of the dominant is IV/V or S/D.
Inverted intervals
An interval is inverted by raising or lowering either of the notes the necessary number of octaves, so that both retain their names (pitch class) and the one which was higher is now lower and vice versa, changing the perspective or relation between the pitch classes. For example, the inversion of an interval consisting of a C with an E above it is an E with a C above it - to work this out, the C may be moved up, the E may be lowered, or both may be moved.
Under inversion, perfect intervals remain perfect, major intervals become minor and the reverse, augmented intervals become diminished and the reverse. (Double diminished intervals become double augmented intervals, and the reverse.) Traditional interval names sum to nine: seconds become sevenths and the reverse, thirds become sixes and the reverse, and fourths become fifths and the reverse. Thus a perfect fourth becomes a perfect fifth, an augmented fourth becomes a diminished fifth, and a simple interval (that is, one that is narrower than an octave) and its inversion, when added together, will equal an octave. See also complement (music).
Inversion in counterpoint
When applied to counterpoint, a contrapuntal inversion of two melodies simultaneously being played by two voices is the switching of the melodies between voices, so that the upper voice melody is now played in the lower voice, and vice versa.
Inverted melodies
When applied to melodies, the inversion of a given melody is the melody turned upside-down. For instance, if the original melody has a rising major third (see interval), the inverted melody has a falling major third (or perhaps more likely, in tonal music, a falling minor third, or even some other falling interval). Similarly, in twelve-tone technique, the inversion of the tone row is the so-called prime series turned upside-down.
Inversional equivalency
Inversional equivalency is the concept that intervals, chords, and other sets of pitches are the same when inverted. It is similar to enharmonic equivalency and octave equivalency and even transpositional equivalency. Inversional equivalency is used little in tonal theory, though it is assumed a set which may be inverted onto another are remotely in common. However, taking them to be identical or near-identical is only assumed in musical set theory.
Inversion in musical set theory
In musical set theory inversion may be usefully thought of as the compound operation transpositional inversion, which is the same sense of inversion as in the Inverted melodies section above, with transposition carried out after inversion. Pitch inversion by an ordered pitch interval may be defined as:
- <math> T^p_nI = -x+n <math>
which equals
- <math> T^p_nI = n-x <math>
First invert the pitch or pitches, x=-x, then transpose, -x+n.
Pitch class inversion by a pitch class interval may be defined as:
- <math>T_nI(x) = -x+n\ (mod 12)<math>